MLP
آموزش شبکه عصبی از پایه در پایتون
کتابخانه یادگیری ماشینی خود را بسازید.
در این مقاله ریاضیات یادگیری ماشین و کد را از ابتدا در پایتون مرور خواهیم کرد، یک کتابخانه کوچک برای ساخت شبکه های عصبی با لایه های مختلف (کاملا متصل، کانولوشن یا هم پیچشی (Convolutional) و غیره). در نهایت، ما قادر خواهیم بود شبکه هایی را به صورت مدولار یا پودمانی (modular) ایجاد کنیم:
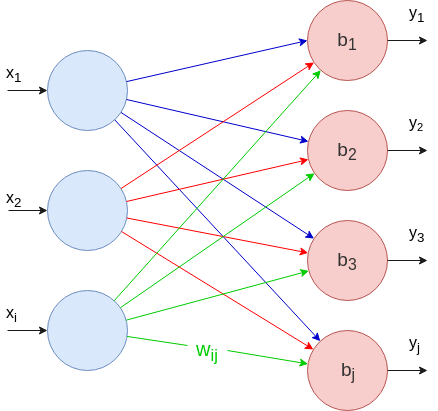
شبکه عصبی 3 لایه ای
فرض می شود شما قبلا اطلاعاتی در مورد شبکه های عصبی دارید. در اینجا هدف توضیح این نیست که چرا این مدل ها را می سازیم، بلکه نشان دادن نحوه اجرای صحیح است.
لایه به لایه
در اینجا باید تصویر بزرگ را در نظر داشته باشیم:
- ما داده های ورودی را به شبکه عصبی تغذیه می کنیم.
- داده ها از لایه ای به لایه دیگر جریان می یابد تا زمانی که خروجی داشته باشیم.
- وقتی خروجی داشتیم، میتوانیم خطا را محاسبه کنیم که یک اسکالر (scalar) است.
- در نهایت می توانیم یک پارامتر معین (وزن یا سوگیری) را با کم کردن مشتق خطا نسبت به خود پارامتر تنظیم کنیم.
- ما از طریق آن فرآیند تکرار می کنیم.
مهمترین مرحله، مرحله چهارم است. ما میخواهیم قادر باشیم هر تعداد لایه، از هر نوع که می خواهیم، داشته باشیم. اما اگر یک لایه را از شبکه اصلاح / افزودن / حذف کنیم، خروجی شبکه تغییر می کند، که خطا را تغییر می دهد، که باعث تغییر مشتق خطا نسبت به پارامتر ها می شود. ما باید بتوانیم مشتقات را بدون توجه به معماری شبکه، صرف نظر از توابع فعال سازی و بدون توجه به ضرری که استفاده می کنیم، محاسبه کنیم.
برای رسیدن به این هدف، باید هر لایه را جداگانه پیاده سازی کنیم.
آنچه که هر لایه باید پیاده سازی کند
هر لایه ای که ممکن است ایجاد کنیم (کاملا متصل، کانولوشن، حداکثر تجمع یا maxpooling، حذف شدن یا dropout و غیره) حداقل دو چیز مشترک دارند: داده های ورودی و خروجی.
انتشار رو به جلو
نکته مهمی که می توانیم تأکید کنیم این است که: خروجی یک لایه ورودی لایه بعدی است.
به این انتشار رو به جلو گفته می شود. در اصل، داده های ورودی را به لایه اول می دهیم، سپس خروجی هر لایه به ورودی لایه بعدی تبدیل می شود تا زمانی که به انتهای شبکه برسیم. با مقایسه نتیجه شبکه (Y) با خروجی مورد نظر (Y* در نظر می گیریم)، می توانیم خطای E را محاسبه کنیم. هدف این است که با تغییر پارامتر های شبکه، این خطا را به حداقل برسانیم؛ یعنی انتشار به عقب (پس انتشار).
گرادیان نزول
این یک یادآوری سریع است، اگر نیاز به یادگیری بیشتر در مورد نزول گرادیان دارید، منابع زیادی در اینترنت وجود دارد.
اساسا می خواهیم پارامتری را در شبکه تغییر دهیم (به آن w می گوییم) تا کل خطای E کاهش یابد. یک راه هوشمندانه برای انجام آن (نه تصادفی) وجود دارد که به شرح زیر است:
جایی که α پارامتری در محدوده [0,1] می باشد که آن را تنظیم می کنیم و به آن نرخ یادگیری می گویند. به هر حال، نکته مهم در اینجا w∂E/∂ (مشتق E نسبت به w) است. ما باید بتوانیم مقدار آن عبارت را برای هر پارامتری از شبکه بدون توجه به معماری آن پیدا کنیم.
انتشار به عقب
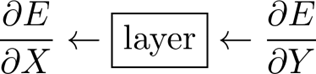
فرض کنید به یک لایه، مشتق خطا را نسبت به خروجی آن می دهیم (E/∂Y∂)، پس باید بتواند مشتق خطا را نسبت به ورودی خود (E/∂X∂) ارائه دهد.
به یاد داشته باشید که E یک اسکالر (یک عدد) است و X و Y ماتریس هستند.
فعلا E/∂X∂ را فراموش کنیم. ترفند این است که اگر به E/∂Y∂ دسترسی داشته باشیم، می توانیم به راحتی E/∂W∂ (اگر لایه دارای پارامتر های قابل آموزش باشد) را بدون دانستن چیزی در مورد معماری شبکه محاسبه کنیم! ما به سادگی از قانون زنجیره ای استفاده می کنیم:
این فرمول بسیار مهم است، زیرا کلید درک پس انتشار است! پس از آن، ما قادر خواهیم بود در کمترین زمان یک شبکه عصبی پیچیده عمیق را از ابتدا کد نویسی کنیم!
نمودار برای درک پس انتشار
این همان چیزی است که قبلا توضیح داده شده است. لایه 3 قرار است پارامتر های خود را با استفاده از Y∂ ∂E/به روز کند و سپس E /∂H2∂ را به لایه قبلی، که “E/∂Y∂” خودش است، ارسال می کند. سپس لایه 2 همین کار را انجام می دهد و غیره.
این ممکن است در اینجا انتزاعی به نظر برسد، اما زمانی که ما آن را برای نوع خاصی از لایه اعمال کنیم، بسیار واضح خواهد شد. وقتی صحبت از انتزاعی شد، اکنون زمان خوبی برای نوشتن اولین طبقه (کلاس) پایتون است.
کلاس پایه چکیده: لایه
طبقه انتزاعی Layer، که تمام لایه های دیگر از آن به ارث میبرند، ویژگی های ساده ای را مدیریت می کند که یک ورودی، یک خروجی، و هر دو روش رو به جلو و عقب هستند.
|
1 # Base class 2 class Layer: 3 def __init__(self): 4 self.input = None 5 self.output = None 6 7 # computes the output Y of a layer for a given input X 8 def forward_propagation(self, input): 9 raise NotImplementedError 10 11 # computes dE/dX for a given dE/dY (and update parameters if any) 12 def backward_propagation(self, output_error, learning_rate): 13 raise NotImplementedError |
اشاره نکردم، که آن learning_rate می باشد. این پارامتر باید چیزی شبیه یک خط مشی به روز رسانی یا همان طور که در Keras به آن می گویند یک بهینه ساز باشد، اما برای سادگی ما می خواهیم از نرخ یادگیری بگذریم و پارامتر های خود را با استفاده از گرادیان نزول به روز کنیم.
لایه کاملا متصل (Fully Connected Layer)
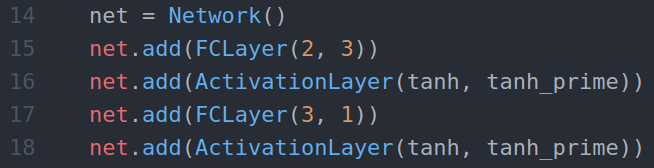
حال بیایید اولین نوع لایه را تعریف و پیاده سازی کنیم: لایه کاملا متصل یا لایه FC. لایه های FC اساسی ترین لایه ها هستند، زیرا هر نورون ورودی به هر نورون خروجی متصل است.
انتشار رو به جلو
مقدار هر نورون خروجی را می توان به صورت زیر محاسبه کرد:
با ماتریس ها، می توانیم این فرمول را برای هر نورون خروجی در یک نوبت با استفاده از ضرب (حاصلضرب) نقطه ای (dot product) محاسبه کنیم.
کارمان با انتقال (pass) رو به جلو تمام شد. حال اجازه دهید انتقال رو به عقب لایه FC را انجام دهیم.
000
توجه داشته باشید که من هنوز از هیچ تابع فعال سازی استفاده نمی کنم، به این دلیل است که آن را در یک لایه جداگانه پیاده سازی می کنیم!
000



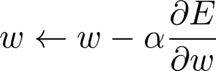
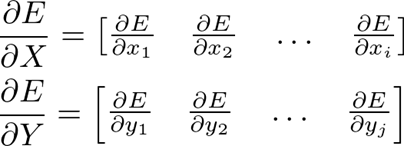
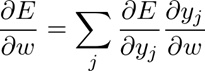

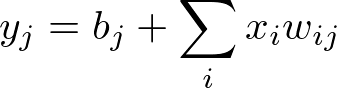
دیدگاهتان را بنویسید