keras
بررسی کلی
- شبکه های عصبی یکی از محبوب ترین الگوریتم های یادگیری ماشینی می باشند
- گرادیان کاهشی (Gradient Descent) اساس شبکه های عصبی را تشکیل می دهد
- شبکه های عصبی را می توان در R و پایتون با استفاده از کتاب خانه ها و بسته های خاصی پیاده سازی کرد
مقدمه
شما می توانید یک مفهوم را به دو روش یاد بگیرید و تمرین کنید:
- گزینه اول: می توانید کل نظریه را در مورد یک موضوع خاص یاد بگیرید و سپس به دنبال راه هایی برای به کارگیری آن مفاهیم باشید. بنابراین، نحوه عملکرد یک الگوریتم کامل، ریاضیات پشت آن، فرضیه ها و محدودیت های آن را می خوانید و سپس آن را اعمال می کنید. رویکردی قوی اما وقت گیر.
- گزینه دوم: با اصول اولیه ساده شروع کنید و شهودی در مورد موضوع ایجاد کنید. سپس، یک مشکل را انتخاب کنید و شروع به حل آن کنید. در حین حل مشکل، مفاهیم را بیاموزید. سپس، به اصلاح و بهبود درک خود ادامه دهید. بنابراین، نحوه اعمال یک الگوریتم را بخوانید – بیرون بروید و آن را اعمال کنید. هنگامی که می دانید چگونه آن را اعمال کنید، آن را با پارامتر ها، مقادیر، محدودیت های مختلف امتحان کنید و درک درستی از الگوریتم ایجاد کنید.
من گزینه دوم را ترجیح می دهم و برای یادگیری هر موضوع جدیدی از آن رویکرد استفاده می کنم.
من ممکن است نتوانم تمام ریاضیات پشت یک الگوریتم را به شما بگویم، اما می توانم شهود را به شما بگویم. من می توانم بهترین سناریو ها را برای اعمال یک الگوریتم بر اساس تجربیات و درک خود به شما بگویم.
در تعاملم با مردم، متوجه می شوم که مردم برای توسعه این شهود وقت نمی گذارند و از این رو آنها برای بانجام این ها به شیوه ای درست، تقلای بسیاری می کنند.
در این مقاله، من بلوک ساختمان شبکه های عصبی را از ابتدا مورد بحث قرار می دهم و بیشتر بر توسعه این شهود برای اعمال شبکه های عصبی تمرکز می کنم. ما هم با پایتون و هم با R کد می نویسیم. در پایان این مقاله، نحوه عملکرد شبکه های عصبی، نحوه اولیه سازی وزن ها و نحوه بهروزرسانی آن ها را با استفاده از انتشار به عقب (back-propagation) خواهید فهمید.
بیایید شروع کنیم.
اگر می خواهید این را در قالب دوره یاد بگیرید، دوره اساس یادگیری عمیق ما را بررسی کنید
فهرست مطالب:
- شهود ساده پشت شبکه های عصبی
- پرسپترون (Perception) چند لایه و اصول اولیه آن
- مراحل دخیل در روش شناسی شبکه عصبی
- تجسم مراحل برای روش کار شبکه عصبی
- پیاده سازی NN با استفاده از Numpy(پایتون)
- پیاده سازی NN با استفاده از R
- درک دقیق پیاده سازی شبکه های عصبی از پایه با جزئیات
- [اختیاری] دیدگاه ریاضی الگوریتم انتشار برگشتی
شهود ساده در پشت شبکه های عصبی
در صورتی که توسعه دهنده بوده باشید یا یک اثر را دیده باشید – می دانید که چگونه می توانید اشکالات را در کد جستجو کنید. با تغییر ورودی ها یا شرایط، حالت های مختلف تست را اجرا می کنید و به دنبال خروجی می گردید. علاوه بر این، تغییر در خروجی به شما راهنمایی می کند که کجا به دنبال اشکال بگردید – کدام ماژول را بررسی کنید، یا کدام خطوط را بخوانید. هنگامی که آن را پیدا کردید، تغییرات را ایجاد می کنید و تمرین تا زمانی که کد/برنامه مناسب را داشته باشید ادامه می یابد.
شبکه های عصبی به شیوه ای بسیار مشابه کار می کنند. چندین ورودی می گیرند، آن را از طریق نورون های متعدد از چندین لایه پنهان پردازش می کنند و نتیجه را با استفاده از یک لایه خروجی برمی گرداند. این فرآیند تخمین نتیجه از نظر فنی به عنوان “انتشار رو به جلو” شناخته می شود.
در مرحله بعد، نتیجه را با خروجی واقعی مقایسه می کنیم. وظیفه این است که خروجی شبکه عصبی نزدیک به خروجی واقعی (مد نظر) باشد. هر یک از این نورون ها در خروجی نهایی با خطا همراه هستند. چگونه خطا را کاهش خواهید داد؟
ما سعی میکنیم ارزش/ وزن نورون هایی را که بیشتر در بروز خطا نقش دارند، به حداقل برسانیم و این هنگام بازگشت به نورون های شبکه عصبی و یافتن محل خطا رخ می دهد. این فرآیند به عنوان “انتشار به عقب” شناخته می شود.
به منظور کاهش این تعداد تکرار برای به حداقل رساندن خطا، شبکه های عصبی از یک الگوریتم رایج به نام “Gradient Descent” یا گرادیان کاهشی استفاده می کنند که به بهینه سازی سریع و کارآمد وظیفه کمک می کند.
همینه – شبکه های عصبی این گونه کار می کنند! من می دانم که این یک ارائه بسیار ساده است، اما به شما کمک می کند تا مسائل را به روشی ساده درک کنید.
پرسپترون چند لایه و اصول آن
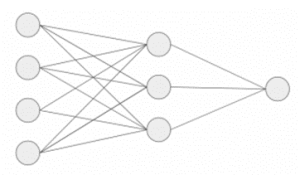
درست مانند اتم ها که اساس هر ماده روی زمین را تشکیل می دهند – واحد تشکیل دهنده اصلی شبکه عصبی یک پرسپترون است. بنابراین، پرسپترون چیست؟
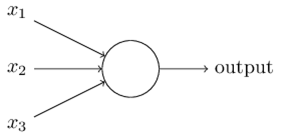
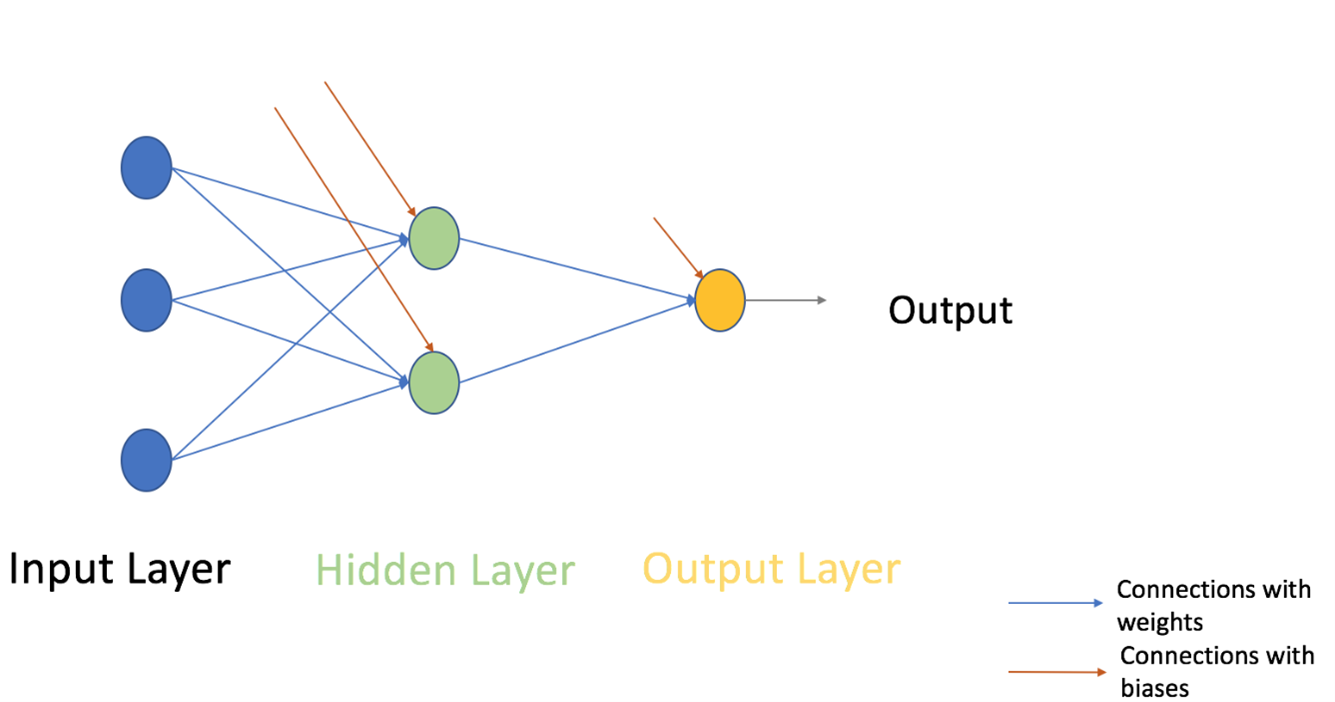
پرسپترون را می توان به عنوان هر چیزی که چندین ورودی می گیرد و یک خروجی تولید می کند مفهوم کرد. برای مثال به تصویر زیر نگاه کنید.
پرسپترون
ساختار فوق سه ورودی می گیرد و یک خروجی تولید می کند. سوال منطقی بعدی این است که چه رابطه ای بین ورودی و خروجی وجود دارد؟ اجازه دهید با روش های اساسی شروع کنیم و راه های پیچیده تری را پیدا کنیم.
در ذیل، من سه راه ایجاد روابط ورودی-خروجی را مورد بحث قرار داده ام:
- با ترکیب مستقیم ورودی و محاسبه خروجی بر اساس مقدار آستانه. به عنوان مثال: x1=0, x2=1, x3=1 را در نظر بگیرید و یک آستانه =0 را تعیین کنید. بنابراین، اگر x1+x2+x3>0 باشد، خروجی 1 در غیر این صورت 0 است. می بینید که در این حالت، پرسپترون خروجی را 1 محاسبه می کند.
- در مرحله بعد، وزن ها را به ورودی ها اضافه می کنیم. وزن ها به یک ورودی، اهمیت می دهند. برای مثال، w1=2, w2=3 و w3=4 را به ترتیب به x1, x2 و x3 اختصاص می دهید. برای محاسبه خروجی، ورودی را با وزن های مربوطه ضرب می کنیم و با مقدار آستانه به صورت w1*x1 + w2*x2 + w3*x3 > آستانه مقایسه می کنیم. این وزن ها در مقایسه با x1 و x2 به x3 اهمیت بیشتری می دهند.
- در مرحله بعد، سوگیری را اضافه می کنیم: هر پرسپترون همچنین دارای یک سوگیری است که می توان آن را مقدار انعطاف پذیری پرسپترون در نظر گرفت. این پرسپترون تا حدی شبیه ثابت b تابع خطی y = ax + b است. این به ما امکان می دهد تا برای تطبیق بهتر پیش بینی با داده ها، صف آرایی را به سمت پایین حرکت دهیم. بدون b خط همیشه از مبدأ (0, 0) عبور می کند و ممکن است تناسب ضعیف تری داشته باشید. به عنوان مثال، یک پرسپترون ممکن است دو ورودی داشته باشد، در این صورت، به سه وزن نیاز دارد؛ یکی، برای هر ورودی و دیگری برای سوگیری. اکنون نمایش خطی ورودی مانند w1*x1 + w2*x2 + w3*x3 + 1*bخواهد بود.
اما، همه اینها هنوز خطی هستند، همان چیزی که پرسپترون ها قبلا بودند. اما آن چنان هم سرگرم کننده نبود. بنابراین، مردم به فکر تکامل یک پرسپترون به چیزی بودند که امروزه به عنوان یک نورون مصنوعی نامیده می شود. یک نورون، تبدیل های غیر خطی (تابع فعال سازی) را به ورودی ها و سو گیری ها اعمال می کند.
تابع فعال سازی چیست؟
تابع فعال سازی مجموع ورودی وزنی (w1*x1 + w2*x2 + w3*x3 + 1*b) را به عنوان آرگومان می گیرد و خروجی نورون را برمی گرداند.
در معادله بالا 1 را x0 و b را w0 نشان داده ایم.
علاوه بر این، تابع فعال سازی بیشتر برای ایجاد یک تبدیل غیر-خطی استفاده می شود که به ما امکان می دهد فرضیه های غیرخطی را برازش دهیم، یا توابع پیچیده را تخمین بزنیم. چندین توابع فعال سازی مانند “Sigmoid”، “Tanh”، ReLu و بسیاری دیگر وجود دارد.
انتشار رو به جلو، انتشار به عقب، و دوره ها
تاکنون خروجی را محاسبه کرده ایم و این فرآیند به نام «انتشار رو به جلو» شناخته می شود. اما اگر خروجی تخمین زده شده با خروجی واقعی فاصله زیادی داشته باشد (خطای زیاد)، چه اتقاقی می افتد؟ در شبکه عصبی کاری که انجام می دهیم، سوگیری ها و وزن ها را بر اساس خطا به روز می کنیم. این روند به روز رسانی وزن و سوگیری به عنوان “انتشار به عقب” شناخته می شود.
الگوریتم های انتشار به عقب (BP) با تعیین ضرر (یا خطا) در خروجی و سپس انتشار مجدد آن به شبکه کار می کنند. وزن ها برای به حداقل رساندن خطای ناشی از هر نورون به روز می شوند. پس از آن، اولین گام در به حداقل رساندن خطا، تعیین گرادیان (مشتقات) هر گره خروجی نهایی w.r.t است. برای دریافت دیدگاه ریاضی از انتشار به عقب، به بخش زیر مراجعه کنید.
این یک دور تکرار ارسال و انتشار به عقب، به عنوان یک تکرار آموزشی با نام “Epoch” (دوره) شناخته می شود.
پرسپترون چند لایه
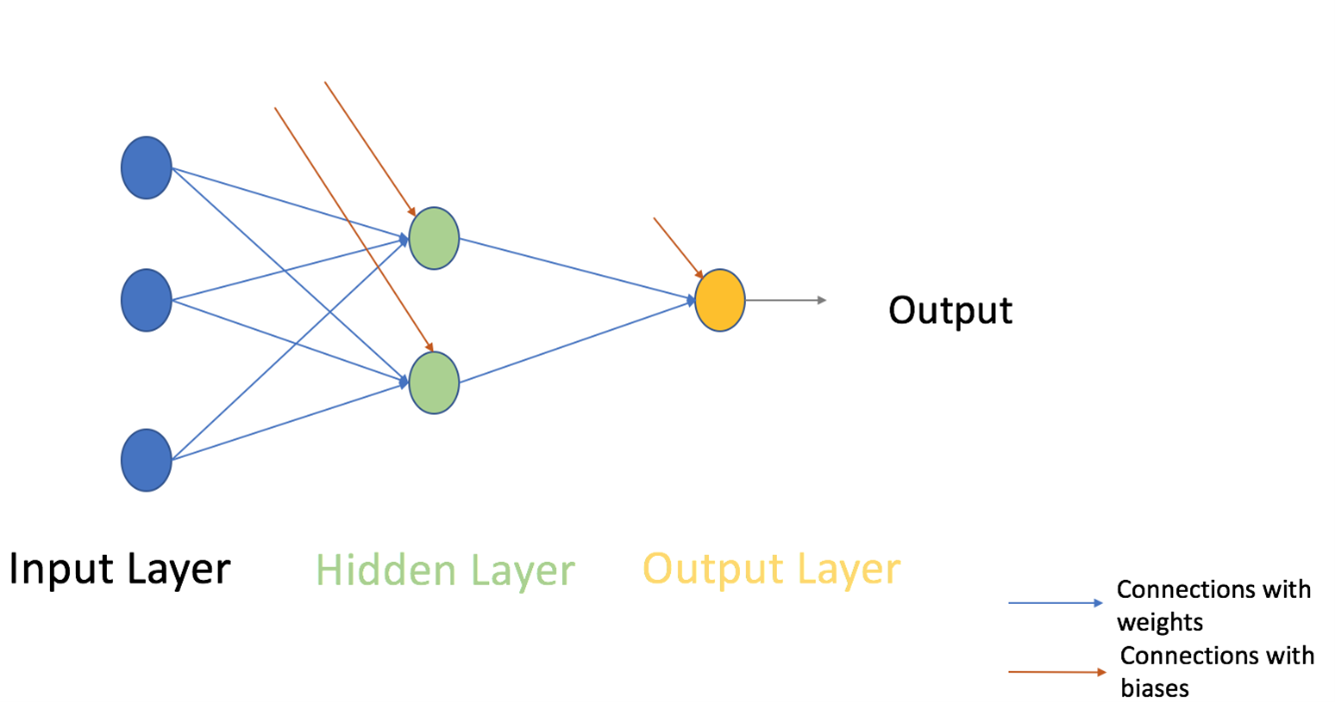
حال بیایید به قسمت بعدی پرسپترون چند لایه برویم. تا کنون، ما فقط یک لایه متشکل از 3 گره ورودی یعنی x1، x2 و x3 و یک لایه خروجی متشکل از یک نورون واحد را دیده ایم. اما، برای اهداف عملی، تنها شبکه تک لایه می تواند کاربردی باشد. یک MLP از لایه های متعددی به نام لایه های پنهان تشکیل شده است که بین لایه ورودی و لایه خروجی مطابق شکل زیر، انباشته شده اند.
تصویر بالا فقط یک لایه پنهان را به رنگ سبز نشان می دهد، اما در عمل می تواند چندین لایه پنهان داشته باشد. علاوه بر این، نکته دیگری که در مورد MLP باید به خاطر بسپارید این است که همه لایه ها به طور کامل متصل هستند، یعنی هر گره در یک لایه (به جز لایه ورودی و خروجی) به هر گره در لایه قبلی و لایه بعدی متصل است.
بیایید به موضوع بعدی برویم که یک الگوریتم آموزشی برای شبکه های عصبی است (برای به حداقل رساندن خطا). در اینجا، ما به رایج ترین الگوریتم های آموزشی معروف به Gradient descent نگاه می کنیم.
نزول گرادیان کامل دسته ای و نزول گرادیان تصادفی
هر دو نوع نزول گرادیان کار یکسانی را برای به روز رسانی وزن های MLP با استفاده از الگوریتم به روز رسانی یکسان انجام می دهند، اما تفاوت در تعداد نمونه های آموزشی مورد استفاده برای به روز رسانی وزن ها و سوگیری ها نهفته است. الگوریتم Full Batch Gradient Descent یا نزول گرادیان کامل دسته ای، همان طور که از نام آن پیداست از تمام نقاط داده آموزشی برای به روز رسانی هر یک از وزن ها برای یک بار استفاده می کند در حالی که گرادیان تصادفی از 1 (نمونه) یا بیشتر استفاده می کند اما هرگز از کل داده های آموزشی برای به روز رسانی وزن ها برای یک بار استفاده نمی کند.
اجازه دهید این را با یک مثال ساده از یک مجموعه داده شامل 10 نقطه داده با دو وزن w1 و w2 درک کنیم.
دسته کامل: شما از 10 نقطه داده (کل داده های آموزشی) استفاده می کنید و تغییر در w1 (Δw1) و w2 (Δw2) را محاسبه می کنید و w1 و w2 را به روز می کنید.
SGD: شما از نقطه داده اول استفاده می کنید و تغییر w1 (Δw1) و تغییر در w2 (Δw2) را محاسبه می کنید و w1 و w2 را به روز می کنید. در مرحله بعد، وقتی از نقطه داده دوم استفاده می کنید، روی وزن های به روز شده کار خواهید کرد.
برای توضیح بیشتر در مورد هر دو روش، می توانید به این مقاله نگاهی بیندازید.
مراحل دخیل در روش شناسی شبکه عصبی
بیایید به روش سازی گام به گام شبکه عصبی (MLP با یک لایه پنهان، شبیه به ساختار عکس فوق نشان داده شده) نگاه کنیم. در لایه خروجی، ما تنها یک نورون داریم که در حال حل یک مسئله طبقه بندی دودویی هستیم (پیش بینی ۰ یا ۱). ما همچنین می توانستیم دو نورون برای پیش بینی هر یک از هر دو طبقه داشته باشیم.
ابتدا به مراحل متنوع و جامع نگاه کنید:
- 0. ورودی و خروجی را می گیریم
- X به عنوان یک ماتریس ورودی
- y به عنوان یک ماتریس خروجی
- 1. سپس وزن ها و سوگیری ها را با مقادیر تصادفی اولیه سازی می کنیم (این اولیه سازی یک بار است. در ادامه، از وزن ها و سوگیری های به روز شده استفاده خواهیم کرد). اجازه دهید تعریف کنیم:
- wh به عنوان یک ماتریس وزن برای لایه پنهان
- bh به عنوان ماتریس سوگیری برای لایه پنهان
- wout به عنوان یک ماتریس وزن برای لایه خروجی
- bout به عنوان ماتریس سوگیری برای لایه خروجی
2.) سپس ما ماتریس نقطه، محصول ورودی و وزن اختصاص داده شده به لبه های بین ورودی و لایه پنهان را به دست می آوریم و سپس سوگیری های نورون های لایه پنهان را به ورودی مربوطه اضافه می کنیم، این به عنوان تبدیل خطی شناخته می شود:
- 3. تبدیل غیر-خطی را با استفاده از یک تابع فعال سازی (Sigmoid) انجام دهید. Sigmoid خروجی را به صورت 1/(1 + exp(-x)) برمی گرداند.
- 4. سپس یک تبدیل خطی روی لایه پنهان فعال سازی انجام دهید (محصول نقطه ماتریس را با وزن ها به دست آورید و یک سوگیری از نورون لایه خروجی اضافه کنید) سپس یک تابع فعال سازی اعمال کنید (دوباره از سیگموید استفاده می شود، اما می توانید از هر تابع فعال سازی دیگری بسته به وظیفه خود استفاده کنید) تا خروجی را پیش بینی کند.
تمام مراحل فوق به عنوان “انتشار رو به جلو” شناخته می شوند.
- 5. پیش بینی را با خروجی واقعی مقایسه کنید و گرادیان خطا را محاسبه کنید (هم خطای واقعی و هم پیش بینی شده).
خطا میانگین مربعات تلفات= ((Y-t)^2)/2.
E = y – output
- 6. شیب/ گرادیان نورون های لایه پنهان و خروجی را محاسبه کنید (برای محاسبه شیب، مشتقات فعال سازی های غیر-خطی x را در هر لایه برای هر نورون محاسبه می کنیم). گرادیان سیگموئید را می توان به صورت x * (1 – x) برگرداند.
slope_output_layer = derivatives_sigmoid(output)
slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
- 7. سپس ضریب تغییر (مثلث یا دلتا) را در لایه خروجی محاسبه کنید، وابسته به گرادیان خطای ضرب شده در شیب فعال سازی لایه خروجی
d_output = E * slope_output_layer
- 8. در این مرحله، خطا دوباره در شبکه منتشر می شود که به معنای خطا در لایه پنهان است. برای این کار، حاصل ضرب نقطه ای دلتای لایه خروجی را با پارامتر های وزنی لبه های بین لایه پنهان و خروجی (T) می گیریم.
Error_at_hidden_layer = matrix_dot_product(d_output, wout.Transpose)
- 9. ضریب تغییر (دلتا) را در لایه پنهان محاسبه کنید، خطا را در لایه پنهان با شیب فعال سازی لایه پنهان ضرب کنید.
d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
- 10. سپس وزن ها را در لایه های خروجی و پنهان به روز رسانی کنید: وزن های موجود در شبکه را می توان از خطا های محاسبه شده برای مثال (های) آموزشی به روز رسانی کرد.
wout = wout + matrix_dot_product(hiddenlayer_activations.Transpose, d_output)*learning_rate
wh = wh + matrix_dot_product(X.Transpose,d_hiddenlayer)*learning_rate
نرخ-یادگیری: مقداری که وزن ها به روز شده توسط یک پارامتر پیکر بندی به نام نرخ یادگیری کنترل می شود.
- 11. در نهایت، سو گیری ها را در لایه خروجی و پنهان به روز رسانی کنید: سو گیری ها در شبکه را می توان از روی خطا های انباشته در آن نورون به روز رسانی کرد.
- سو گیری در لایه_خروجی = سو گیری در لایه_خروجی + مجموع دلتای لایه_خروجی بر حسب ردیف * نرخ_یادگیری
- سو گیری در لایه پنهان = سوگیری در لایه پنهان + مجموع دلتای لایه خروجی در ردیف * نرخ_یادگیری
bh = bh + sum(d_hiddenlayer, axis=0) * learning_rate
bout = bout + sum(d_output, axis=0)*learning_rate
مراحل 5 تا 11 به عنوان “انتشار به عقب” شناخته می شوند.
یک تکرار انتشار به جلو و عقب به عنوان یک چرخه آموزشی در نظر گرفته می شود. همانطور که قبلا اشاره شده است، زمانی که برای بار دوم آموزش می دهیم، پس از آن وزن ها و سو گیری های به روز شده برای انتشار رو به جلو استفاده می شود.
در بالا، وزن و سو گیری ها را برای لایه پنهان و خروجی به روز رسانی کرده ایم و از یک الگوریتم نزول گرادیان دسته ای کامل استفاده کرده ایم.
تجسم مراحل برای روش شناسی شبکه عصبی
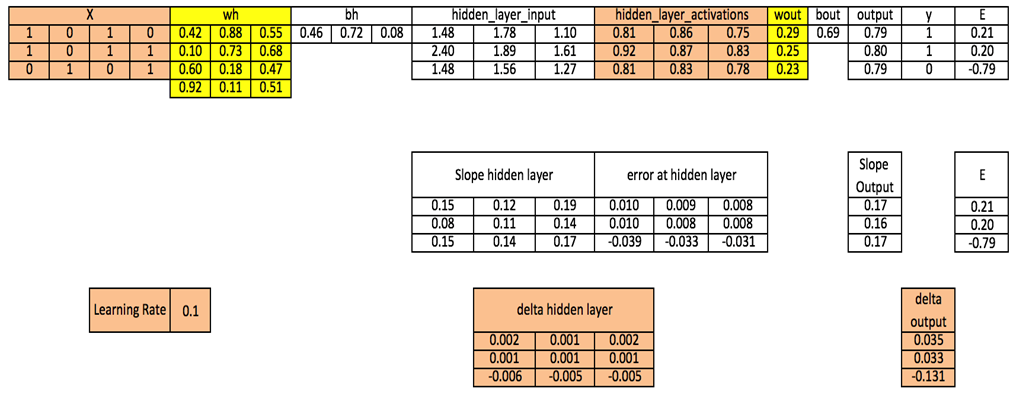
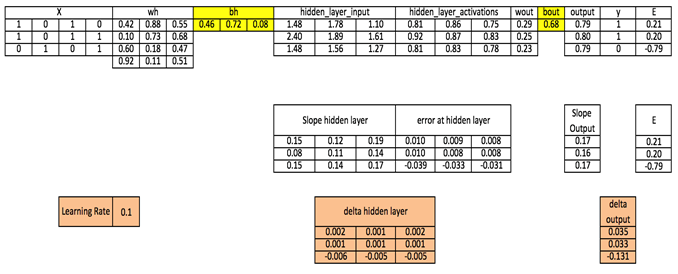
ما مراحل بالا را تکرار می کنیم و ورودی، وزن ها، سو گیری ها، خروجی ها، ماتریس خطا را برای درک روش کار شبکه عصبی (MLP) تجسم می کنیم.
توجه داشته باشید:
- برای تجسم تصاویر به خوبی، من موقعیت های اعشاری را در موقعیت های 2 یا 3 گرد کرده ام.
- سلول های زرد نشان دهنده سلول فعال فعلی است
- سلول نارنجی نشان دهنده ورودی مورد استفاده برای پر کردن مقادیر سلول فعلی است
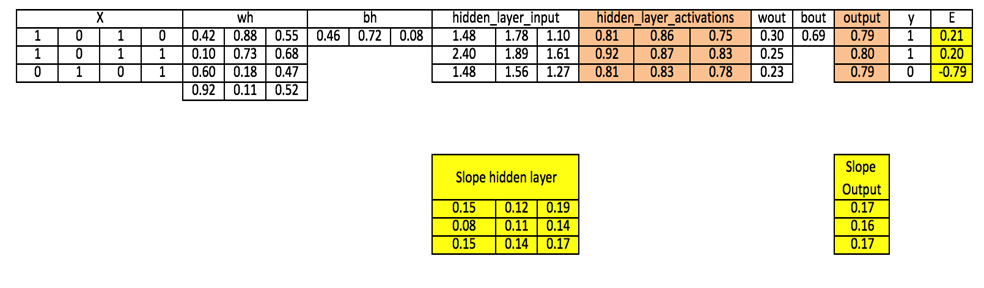
مرحله 0 : ورودی و خروجی را بخوانید
مرحله 1: وزن ها و سو گیری ها را با مقادیر تصادفی اولیه سازی کنید (روش هایی برای مقدار دهی اولیه وزن ها و سو گیری ها وجود دارد اما در حال حاضر با مقادیر تصادفی مقدار دهی اولیه می شود)
مرحله 2: ورودی لایه پنهان را محاسبه کنید:
hidden_layer_input= matrix_dot_product(X,wh) + bh
مرحله 3: تبدیل غیر-خطی را روی ورودی خطی پنهان انجام دهید
hiddenlayer_activations = sigmoid(hidden_layer_input)
مرحله 4: تبدیل خطی و غیر-خطی فعال سازی لایه پنهان را در لایه خروجی انجام دهید
output_layer_input = matrix_dot_product (hiddenlayer_activations * wout ) + bout
output = sigmoid(output_layer_input)
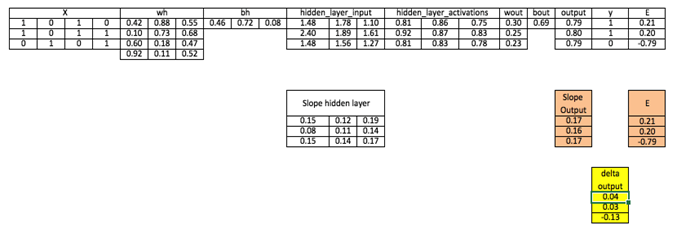
مرحله 5: گرادیان خطا (E) را در لایه خروجی محاسبه کنید
E = y-output
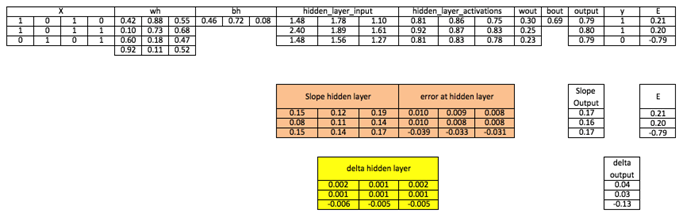
مرحله 6: شیب در خروجی و لایه پنهان را محاسبه کنید
Slope_output_layer= derivatives_sigmoid(output)
Slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
مرحله 7: دلتا را در لایه خروجی حساب کنید
d_output = E * slope_output_layer*lr
مرحله 8: خطا را در لایه پنهان محاسبه کنید
d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
مرحله 10: وزن را هم در لایه خروجی و هم در لایه پنهان به روز کنید
wout = wout + matrix_dot_product(hiddenlayer_activations.Transpose, d_output)*learning_rate
wh = wh+ matrix_dot_product(X.Transpose,d_hiddenlayer)*learning_rate
مرحله 11: سو گیری ها را هم در لایه خروجی و هم در لایه پنهان به روز کنید
bh = bh + sum(d_hiddenlayer, axis=0) * learning_rate
bout = bout + sum(d_output, axis=0)*learning_rate
در قسمت فوق، می بینید که هنوز یک خطای خوب وجود دارد که به مقدار هدف واقعی نزدیک نیست زیرا ما فقط یک تکرار آموزشی را تکمیل کرده ایم. اگر چندین بار مدل را آموزش دهیم، به نتیجه واقعی بسیار نزدیک خواهد بود. من هزاران تکرار را تکمیل کرده ام و نتیجه من به مقادیر هدف واقعی نزدیک است ß
([[ 0.98032096] [ 0.96845624] [ 0.04532167]]).
پیاده سازی NN با استفاده از Numpy ) پایتون (
پیاده سازی NN در R
# input matrix
X=matrix(c(1,0,1,0,1,0,1,1,0,1,0,1),nrow = 3, ncol=4,byrow = TRUE)
# output matrix
Y=matrix(c(1,1,0),byrow=FALSE)
#sigmoid function
sigmoid<-function(x){
1/(1+exp(-x))
}
# derivative of sigmoid function
derivatives_sigmoid<-function(x){
x*(1-x)
}
# variable initialization
epoch=5000
lr=0.1
inputlayer_neurons=ncol(X)
hiddenlayer_neurons=3
output_neurons=1
#weight and bias initialization
wh=matrix( rnorm(inputlayer_neurons*hiddenlayer_neurons,mean=0,sd=1), inputlayer_neurons, hiddenlayer_neurons)
bias_in=runif(hiddenlayer_neurons)
bias_in_temp=rep(bias_in, nrow(X))
bh=matrix(bias_in_temp, nrow = nrow(X), byrow = FALSE)
wout=matrix( rnorm(hiddenlayer_neurons*output_neurons,mean=0,sd=1), hiddenlayer_neurons, output_neurons)
bias_out=runif(output_neurons)
bias_out_temp=rep(bias_out,nrow(X))
bout=matrix(bias_out_temp,nrow = nrow(X),byrow = FALSE)
# forward propagation
for(i in 1:epoch){
hidden_layer_input1= X%*%wh
hidden_layer_input=hidden_layer_input1+bh
hidden_layer_activations=sigmoid(hidden_layer_input)
output_layer_input1=hidden_layer_activations%*%wout
output_layer_input=output_layer_input1+bout
output= sigmoid(output_layer_input)
# Back Propagation
E=Y-output
slope_output_layer=derivatives_sigmoid(output)
slope_hidden_layer=derivatives_sigmoid(hidden_layer_activations)
d_output=E*slope_output_layer
Error_at_hidden_layer=d_output%*%t(wout)
d_hiddenlayer=Error_at_hidden_layer*slope_hidden_layer
wout= wout + (t(hidden_layer_activations)%*%d_output)*lr
bout= bout+rowSums(d_output)*lr
wh = wh +(t(X)%*%d_hiddenlayer)*lr
bh = bh + rowSums(d_hiddenlayer)*lr
}
output
درک دقیق پیاده سازی شبکه های عصبی از پایه
اکنون که یک پیاده سازی اساسی numpy را از ابتدا در پایتون و R انجام داده اید، ما عمیقا به درک هر بلوک کد می پردازیم و سعی می کنیم همان کد را در مجموعه داده ای متفاوت اعمال کنیم. همچنین نحوه کار مدل خود را با “اشکال زدایی” گام به گام با استفاده از محیط تعاملی یک نوت بوک jupyter و با استفاده از ابزار های علوم داده پایه مانند numpy و matplotlib، تجسم خواهیم کرد. پس بیایید شروع کنیم!
اولین کاری که انجام می دهیم این است که کتابخانه هایی که پیشتر ذکر شده، یعنی numpy و matplotlib را وارد کنیم. همچنین، همان طور که با IDE نوت بوک jupyter کار خواهیم کرد، رسم درون خطی نمودار ها را با استفاده از تابع جادویی %matplotlib به صورت درون خطی تنظیم خواهیم کرد.
| 1. 1. # importing required libraries |
| 2. 2. %matplotlib inline |
| 3. |
| 4. 4. import numpy as np |
| 5. 5. import matplotlib.pyplot as plt |
بیایید نسخه های کتابخانه هایی را که استفاده می کنیم مورد بررسی قرار بدیم
| 1. 1. # version of numpy library |
| 2. print(“Version of numpy:”, np.__version__) |
Version of numpy: 1.18.1
و همان را برای matplotlib اعمال می کنیم
|
1. # version of matplotlib library |
| 2. import matplotlib |
| 3. |
| 4. print(“Version of matplotlib:”, matplotlib.__version__) |
Version of matplotlib: 3.1.3
همچنین، پارامتر seed تصادفی را روی یک عدد خاص تنظیم می کنیم (مثلا 42 (همان طور که می دانیم این پاسخ همه چیز است!)) تا کدی که اجرا می کنیم هر بار که اجرا می کنیم همان خروجی را به ما بدهد (امیدوارم!)
| 1. # set random seed |
| 2. np.random.seed(42) |
اکنون مرحله بعدی این است که ورودی خود را ایجاد کنیم. ابتدا، بیایید یک مجموعه داده ساختگی را در نظر بگیریم، که در آن ستون اول فقط یک ستون مفید است، در حالی که بقیه ممکن است مفید باشند یا نباشند و می توانند یک نویز بالقوه باشند.
| 1. # creating the input array |
| 2. X = np.array([[1, 0, 0, 0], [1, 0, 1, 1], [0, 1, 0, 1]]) |
| 3. |
| 4. print(“Input:\n”, X) |
| 5. |
| 6. # shape of input array |
| 7. print(“\nShape of Input:”, X.shape) |
این خروجی از اجرای کد بالا است
Input:
[[1 0 0 0]
[1 0 1 1]
[0 1 0 1]]
Shape of Input: (3, 4)
اکنون همان طور که ممکن است به خاطر داشته باشید، ما باید انتقال ورودی را انجام دهیم تا بتوانیم شبکه خود را آموزش دهیم. به سرعت این کار را انجام دهیم
| 1. # converting the input in matrix form |
| 2. X = X.T |
| 3. print(“Input in matrix form:\n”, X) |
| 4. |
| 5. # shape of input matrix |
| 6. print(“\nShape of Input Matrix:”, X.shape) |
Input in matrix form:
[[1 1 0]
[0 0 1]
[0 1 0]
[0 1 1]]
Shape of Input Matrix: (4, 3)
حالا بیایید آرایه خروجی خود را ایجاد کنیم و آن را جابجا کنیم
| 1. # creating the output array |
| 2. y = np.array([[1], [1], [0]]) |
| 3. |
| 4. print(“Actual Output:\n”, y) |
| 5. |
| 6. # output in matrix form |
| 7. y = y.T |
| 8. |
| 9. print(“\nOutput in matrix form:\n”, y) |
| 10. |
| 11. # shape of input array |
| 12. print(“\nShape of Output:”, y.shape) |
اکنون که داده های ورودی و خروجی ما آماده است، بیایید شبکه عصبی خود را تعریف کنیم. ما یک معماری بسیار ساده را تعریف خواهیم کرد که دارای یک لایه پنهان با سه نورون است
| 1. inputLayer_neurons = X.shape[0] # number of features in data set |
| 2. hiddenLayer_neurons = 3 # number of hidden layers neurons |
| 3. outputLayer_neurons = 1 # number of neurons at output layer |
سپس، وزن های هر نورون را در شبکه مقدار دهی اولیه می کنیم. وزن هایی که ایجاد می کنیم دارای مقادیری از 0 تا 1 هستند که در ابتدا به صورت تصادفی مقدار دهی اولیه می کنیم.
برای سادگی کار، ما سوگیری را در محاسبات لحاظ نمی کنیم، اما می توانید پیاده سازی ساده ای را که قبلا انجام دادیم بررسی کنید تا ببینید که چگونه برای عبارت “سوگیری” کار می کند.
| 1. # initializing weight |
| 2. # Shape of weights_input_hidden should number of neurons at input layer * number of neurons at hidden layer |
| 3. weights_input_hidden = np.random.uniform(size=(inputLayer_neurons, hiddenLayer_neurons)) |
| 4. |
| 5. # Shape of weights_hidden_output should number of neurons at hidden layer * number of neurons at output layer |
| 6. weights_hidden_output = np.random.uniform( |
| 7. size=(hiddenLayer_neurons, outputLayer_neurons) |
| 8. ) |
برای وضوح، اشکال این آرایه های numpy را پرینت می کنیم
| 1. # shape of weight matrix |
| 2. weights_input_hidden.shape, weights_hidden_output.shape# We are using sigmoid as an activation function so defining the sigmoid function here |
پس از این، تابع فعال سازی خود را به صورت sigmoid تعریف می کنیم که هم در لایه پنهان و هم در لایه خروجی شبکه استفاده می کنیم.
| 1. # We are using sigmoid as an activation function so defining the sigmoid function here |
| 2. |
| 3. # defining the Sigmoid Function |
| 4. def sigmoid(x): |
| 5. return 1 / (1 + np.exp(-x)) |
و سپس، ما عبور (pass) رو به جلو خود را ابتدا برای فعال سازی لایه پنهان و سپس برای لایه خروجی پیاده سازی می کنیم. عبور رو به جلو ما چیزی شبیه به این خواهد بود
| 1. # hidden layer activations2. |
| 2. |
| 3. hiddenLayer_linearTransform = np.dot(weights_input_hidden.T, X) |
| 4. hiddenLayer_activations = sigmoid(hiddenLayer_linearTransform) |
| 1. # calculating the output |
| 2. outputLayer_linearTransform = np.dot(weights_hidden_output.T, hiddenLayer_activations) |
| 3. output = sigmoid(outputLayer_linearTransform) |
بیایید ببینیم مدل آموزش ندیده ما چه خروجی می دهد.
| 1. # output |
| 2. output |
برای هر نمونه از داده های ورودی یک خروجی دریافت می کنیم. در این مورد، بیایید خطای هر نمونه را با استفاده از مجذور افت خطا (squared error loss) محاسبه کنیم
| 1. # calculating error |
| 2. error = np.square(y – output) / 2 |
| 3. error |
ما خروجی مانند خروجی زیر دریافت می کنیم
ما مرحله انتشار رو به جلو خود را کامل کردیم و خطا را دریافت کردیم. اکنون یک انتشار به عقب انجام خواهیم داد تا خطا را با توجه به وزن هر نورون محاسبه کنیم و سپس این وزن ها را با استفاده از گرادیان نزول ساده به روز کنیم.
ابتدا خطا را با توجه به وزن بین لایه های پنهان و خروجی محاسبه می کنیم. در اصل، ما عملیاتی مانند این را انجام خواهیم داد
برای محاسبه این، موارد زیر مراحل حد متوسط ما برای استفاده از قانون زنجیره است
- نرخ تغییر خطا در خروجی r.t
- نرخ تغییر خروجی r.t Z2
- نرخ تغییر وزن Z2 w.r.t بین لایه پنهانی و خروجی
بیایید عملیات را انجام دهیم
| 1. # rate of change of error w.r.t. output |
| 2. error_wrt_output = -(y – output) |
| 1. # rate of change of output w.r.t. Z2 |
| 2. output_wrt_outputLayer_LinearTransform = np.multiply(output, (1 – output)) |
| 1. # rate of change of Z2 w.r.t. weights between hidden and output layer |
| 2. outputLayer_LinearTransform_wrt_weights_hidden_output = hiddenLayer_activations |
حال، بیایید اشکال عملیات حد واسط را بررسی کنیم.
| 1. # checking the shapes of partial derivatives |
| 2. error_wrt_output.shape, output_wrt_outputLayer_LinearTransform.shape, outputLayer_LinearTransform_wrt_weights_hidden_output.shape |
آنچه ما می خواهیم یک شکل خروجی مانند این است
| 1. # shape of weights of output layer |
| 2. weights_hidden_output.shape |
اکنون همان طور که قبلا دیدیم، می توانیم این عملیات را با استفاده از این معادله به صورت رسمی تعریف کنیم
بیایید مراحل را اجرا کنیم
| 1. # rate of change of error w.r.t weight between hidden and output layer |
| 2. error_wrt_weights_hidden_output = np.dot( |
| 3. outputLayer_LinearTransform_wrt_weights_hidden_output, |
| 4. (error_wrt_output * output_wrt_outputLayer_LinearTransform).T, |
| 5. ) |
| 1. error_wrt_weights_hidden_output.shape |
ما خروجی را همان طور که انتظار می رود دریافت می کنیم.
علاوه بر این، بیایید همان مراحل را برای محاسبه خطا با توجه به وزن های بین لایه های ورودی و پنهان انجام دهیم – مانند زیر
بنابراین توسط قانون زنجیره ای، مراحل حد واسط زیر را محاسبه می کنیم:
- نرخ تغییر خطا در خروجی w.r.t
- نرخ تغییر خروجی w.r.t Z2
- نرخ تغییر Z2 w.r.t فعال سازی لایه پنهان
- نرخ تغییر فعال سازی لایه پنهان w.r.t Z1
- نرخ تغییر وزن Z1 w.r.t بین ورودی و لایه پنهان
| 1. # rate of change of error w.r.t. output |
| 2. error_wrt_output = -(y – output) |
| 1. # rate of change of output w.r.t. Z2 |
| 2. output_wrt_outputLayer_LinearTransform = np.multiply(output, (1 – output)) |
| 1. # rate of change of Z2 w.r.t. hidden layer activations |
| 2. outputLayer_LinearTransform_wrt_hiddenLayer_activations = weights_hidden_output |
| 1. # rate of change of hidden layer activations w.r.t. Z1 |
| 2. hiddenLayer_activations_wrt_hiddenLayer_linearTransform = np.multiply( |
| 3. hiddenLayer_activations, (1 – hiddenLayer_activations) |
| 4. ) |
| 1. # rate of change of Z1 w.r.t. weights between input and hidden layer |
| 2. hiddenLayer_linearTransform_wrt_weights_input_hidden = X |
بیایید اشکال این آرایه های حد واسط را چاپ کنیم
| 1. # checking the shapes of partial derivatives |
| 2. print( |
| 3. error_wrt_output.shape, |
| 4. output_wrt_outputLayer_LinearTransform.shape, |
| 5. outputLayer_LinearTransform_wrt_hiddenLayer_activations.shape, |
| 6. hiddenLayer_activations_wrt_hiddenLayer_linearTransform.shape, |
| 7. hiddenLayer_linearTransform_wrt_weights_input_hidden.shape, |
| 8. ) |
اما آنچه ما می خواهیم آرایه ای از شکل زیر است
| 1. # shape of weights of hidden layer |
| 2. weights_input_hidden.shape |
بنابراین ما آنها را با استفاده از معادله ترکیب می کنیم
| 1. # rate of change of error w.r.t weights between input and hidden layer |
| 2. error_wrt_weights_input_hidden = np.dot( |
| 3. hiddenLayer_linearTransform_wrt_weights_input_hidden, |
| 4. ( |
| 5. hiddenLayer_activations_wrt_hiddenLayer_linearTransform |
| 6. * np.dot( |
| 7. outputLayer_LinearTransform_wrt_hiddenLayer_activations, |
| 8. (output_wrt_outputLayer_LinearTransform * error_wrt_output), |
| 9. ) |
| 10. ).T, |
| 11. ) |
پس این همان خروجی است که ما می خواهیم. بیایید به سرعت شکل آرایه حاصل را بررسی کنیم
| 1. error_wrt_weights_input_hidden.shape |
اکنون مرحله بعدی به روز رسانی پارامتر ها می باشد. برای این کار از تابع به روز رسانی گرادیان وانیل (vanilla gradient) استفاده می کنیم که به شرح زیر است
ابتدا پارامتر آلفا، یعنی نرخ یادگیری را 0.01 تعریف کنید
| 1. # defining the learning rate |
| 2. lr = 0.01 |
همچنین وزن های اولیه را قبل از به روز رسانی چاپ می کنیم
| 1. # initial weights_hidden_output |
| 2. weights_hidden_output |
| 1. # initial weights_input_hidden |
| 2. weights_input_hidden |
| 1. # updating the weights of output layer |
| 2. weights_hidden_output = weights_hidden_output – lr * error_wrt_weights_hidden_output |
و وزن ها را به روز می کنیم
| 1. # updating the weights of hidden layer |
| 2. weights_input_hidden = weights_input_hidden – lr * error_wrt_weights_input_hidden |
سپس وزن ها را دوباره بررسی می کنیم تا ببینیم آیا به روز شده اند یا خیر
| 1. # updated weights_hidden_output |
| 2. weights_hidden_output |
| 1. # updated weights_input_hidden |
| 2. weights_input_hidden |
اکنون، این فقط یک تکرار (یا دوره) از پاس رو به جلو و عقب است. ما باید چندین بار این کار را انجام دهیم تا مدل ما عملکرد بهتری داشته باشد. بیایید مراحل بالا را دوباره برای 1000 دوره انجام دهیم
| 1. # defining the model architecture |
| 2. inputLayer_neurons = X.shape[0] # number of features in data set |
| 3. hiddenLayer_neurons = 3 # number of hidden layers neurons |
| 4. outputLayer_neurons = 1 # number of neurons at output layer |
| 5. |
| 6. # initializing weight |
| 7. weights_input_hidden = np.random.uniform(size=(inputLayer_neurons, hiddenLayer_neurons)) |
| 8. weights_hidden_output = np.random.uniform( |
| 9. size=(hiddenLayer_neurons, outputLayer_neurons) |
| 10. ) |
| 11. |
| 12. # defining the parameters |
| 13. lr = 0.1 |
| 14. epochs = 1000 |
| 1. losses = [] |
| 2. for epoch in range(epochs): |
| 3. ## Forward Propogation |
| 4. |
| 5. # calculating hidden layer activations |
| 6. hiddenLayer_linearTransform = np.dot(weights_input_hidden.T, X) |
| 7. hiddenLayer_activations = sigmoid(hiddenLayer_linearTransform) |
| 8. |
| 9. # calculating the output |
| 10. outputLayer_linearTransform = np.dot( |
| 11. weights_hidden_output.T, hiddenLayer_activations |
| 12. ) |
| 13. output = sigmoid(outputLayer_linearTransform) |
| 14. |
| 15. ## Backward Propagation |
| 16. |
| 17. # calculating error |
| 18. error = np.square(y – output) / 2 |
| 19. |
| 20. # calculating rate of change of error w.r.t weight between hidden and output layer |
| 21. error_wrt_output = -(y – output) |
| 22. output_wrt_outputLayer_LinearTransform = np.multiply(output, (1 – output)) |
| 23. outputLayer_LinearTransform_wrt_weights_hidden_output = hiddenLayer_activations |
| 24. |
| 25. error_wrt_weights_hidden_output = np.dot( |
| 26. outputLayer_LinearTransform_wrt_weights_hidden_output, |
| 27. (error_wrt_output * output_wrt_outputLayer_LinearTransform).T, |
| 28. ) |
| 29. |
| 30. # calculating rate of change of error w.r.t weights between input and hidden layer |
| 31. outputLayer_LinearTransform_wrt_hiddenLayer_activations = weights_hidden_output |
| 32. hiddenLayer_activations_wrt_hiddenLayer_linearTransform = np.multiply( |
| 33. hiddenLayer_activations, (1 – hiddenLayer_activations) |
| 34. ) |
| 35. hiddenLayer_linearTransform_wrt_weights_input_hidden = X |
| 36. error_wrt_weights_input_hidden = np.dot( |
| 37. hiddenLayer_linearTransform_wrt_weights_input_hidden, |
| 38. ( |
| 39. hiddenLayer_activations_wrt_hiddenLayer_linearTransform |
| 40. * np.dot( |
| 41. outputLayer_LinearTransform_wrt_hiddenLayer_activations, |
| 42. (output_wrt_outputLayer_LinearTransform * error_wrt_output), |
| 43. ) |
| 44. ).T, |
| 45. ) |
| 46. |
| 47. # updating the weights |
| 48. weights_hidden_output = weights_hidden_output – lr * error_wrt_weights_hidden_output |
| 49. weights_input_hidden = weights_input_hidden – lr * error_wrt_weights_input_hidden |
| 50. |
| 51. # print error at every 100th epoch |
| 52. epoch_loss = np.average(error) |
| 53. if epoch % 100 == 0: |
| 54. print(f”Error at epoch {epoch} is {epoch_loss:.5f}”) |
| 55. |
| 56. # appending the error of each epoch |
| 57. losses.append(epoch_loss) |
ما یک خروجی مانند این دریافت می کنیم، که یک مرحله اشکال زدایی است که برای بررسی خطا در هر دوره صدم انجام دادیم.
به نظر می رسد مدل ما با ادامه آموزش بهتر و بهتر عمل می کند. بیایید پس از پایان آموزش وزنه ها را بررسی کنیم
| 1. # updated w_ih
|
| 2. weights_input_hidden |
| 1. # updated w_ho |
| 2. weights_hidden_output |
و همچنین یک نمودار برای تجسم نحوه انجام آموزش ترسیم کنید
| 1. # visualizing the error after each epoch |
| 2. plt.plot(np.arange(1, epochs + 1), np.array(losses)) |
آخرین کاری که انجام خواهیم داد این است که بررسی کنیم پیش بینی ها چقدر به خروجی واقعی ما نزدیک هستند
| 1. # final output from the model
|
| 2. output |
| 1. # actual target
|
| 2. y |
تقریبا نزدیک می باشند!
علاوه بر این، کار بعدی که انجام خواهیم داد این است که مدل خود را بر روی یک مجموعه داده متفاوت آموزش دهیم، و عملکرد را با ترسیم یک مرز تصمیم گیری پس از آموزش تجسم کنیم.
بیایید انجام دهیم!
| 1. from sklearn.datasets import make_moons
|
| 2. |
| 3. X, y = make_moons(n_samples=1000, random_state=42, noise=0.1) |
| 1. plt.scatter(X[:, 0], X[:, 1], s=10, c=y) |
ما یک خروجی مانند زیر دریافت می کنیم
| 1. X |
| 1. X -= X.min() |
| 2. X /= X.max() |
| 1. X.min(), X.max() |
| 1. np.unique(y) |
| 1. X.shape, y.shape |
| 1. X = X.T
|
| 2. |
| 3. y = y.reshape(1, -1) |
| 1. X.shape, y.shape |
اکنون شبکه خود را تعریف می کنیم. ما سه فرا پارامتر زیر را بهروز رسانی می کنیم
- نورون های لایه پنهان را به 10 تغییر دهید
- نرخ یادگیری را به 0.1 تغییر دهید
- و برای دوره های بیشتر تمرین کنید
| 1. # defining the model architecture |
| 2. inputLayer_neurons = X.shape[0] # number of features in data set |
| 3. hiddenLayer_neurons = 10 # number of hidden layers neurons |
| 4. outputLayer_neurons = 1 # number of neurons at output layer |
| 5. |
| 6. # initializing weight |
| 7. weights_input_hidden = np.random.uniform(size=(inputLayer_neurons, hiddenLayer_neurons)) |
| 8. weights_hidden_output = np.random.uniform( |
| 9. size=(hiddenLayer_neurons, outputLayer_neurons) |
| 10. ) |
| 11. |
| 12. # defining the parameters |
| 13. lr = 0.1 |
| 14. epochs = 10000 |
| 15. |
| 16. losses = [] |
| 17. for epoch in range(epochs): |
| 18. ## Forward Propogation |
| 19. |
| 20. # calculating hidden layer activations |
| 21. hiddenLayer_linearTransform = np.dot(weights_input_hidden.T, X) |
| 22. hiddenLayer_activations = sigmoid(hiddenLayer_linearTransform) |
| 23. |
| 24. # calculating the output |
| 25. outputLayer_linearTransform = np.dot( |
| 26. weights_hidden_output.T, hiddenLayer_activation |
| 27. ) |
| 28. outputLayer_linearTransform = np.dot(
|
| 29. |
| 30. ## Backward Propagation |
| 31. |
| 32. # calculating error |
| 33. error = np.square(y – output) / 2 |
| 34. |
| 35. # calculating rate of change of error w.r.t weight between hidden and output layer |
| 36. error_wrt_output = -(y – output) |
| 37. output_wrt_outputLayer_LinearTransform = np.multiply(output, (1 – output)) |
| 38. outputLayer_LinearTransform_wrt_weights_hidden_output = hiddenLayer_activations |
| 39. |
| 40. error_wrt_weights_hidden_output = np.dot( |
| 41. outputLayer_LinearTransform_wrt_weights_hidden_output, |
| 42. (error_wrt_output * output_wrt_outputLayer_LinearTransform).T, |
| 43. ) |
| 44. |
| 45. # calculating rate of change of error w.r.t weights between input and hidden laye |
| 46. outputLayer_LinearTransform_wrt_hiddenLayer_activations = weights_hidden_output |
| 47. hiddenLayer_activations_wrt_hiddenLayer_linearTransform = np.multiply( |
| 48. hiddenLayer_activations, (1 – hiddenLayer_activations) |
| 49. ) |
| 50. hiddenLayer_linearTransform_wrt_weights_input_hidden = X |
| 51. error_wrt_weights_input_hidden = np.dot( |
| 52. hiddenLayer_linearTransform_wrt_weights_input_hidden, |
| 53. ( |
| 54. hiddenLayer_activations_wrt_hiddenLayer_linearTransform |
| 55. * np.dot( |
| 56. outputLayer_LinearTransform_wrt_hiddenLayer_activations, |
| 57. (output_wrt_outputLayer_LinearTransform * error_wrt_output), |
| 58. ) |
| 59. ).T, |
| 60. ) |
| 61. |
| 62. # updating the weights |
| 63. weights_hidden_output = weights_hidden_output – lr * error_wrt_weights_hidden_output |
| 64. weights_input_hidden = weights_input_hidden – lr * error_wrt_weights_input_hidden |
| 65. |
| 66. # print error at every 100th epoch |
| 67. epoch_loss = np.average(error) |
| 68. if epoch % 1000 == 0: |
| 69. print(f”Error at epoch {epoch} is {epoch_loss:.5f}”) |
| 70. |
| 71. # appending the error of each epoch |
| 72. losses.append(epoch_loss) |
این خطایی است که ما بعد از هر هزار دوره دریافت می کنیم
و ترسیم آن خروجی مانند این می دهد
| 1. # visualizing the error after each epoch |
| 2. plt.plot(np.arange(1, epochs + 1), np.array(losses)) |
| 1. # final output from the model |
| 2. output[:, :5] |
حال، اگر پیش بینی ها و خروجی ها را به صورت دستی بررسی کنیم، نتیجه به نظر نزدیک می رسد
| 1. y[:, :5] |
سپس، عملکرد را با ترسیم مرز تصمیم گیری تجسم کنید. اشکالی ندارد اگر کد زیر را دنبال نکنید، فعلا می توانید آن را همان طور که هست استفاده کنید.
| 1. # Define region of interest by data limits |
| 2. steps = 1000 |
| 3. x_span = np.linspace(X[0, :].min(), X[0, :].max(), steps) |
| 4. y_span = np.linspace(X[1, :].min(), X[1, :].max(), steps) |
| 5. xx, yy = np.meshgrid(x_span, y_span) |
| 6. |
| 7. # forward pass for region of interest |
| 8. hiddenLayer_linearTransform = np.dot( |
| 9. weights_input_hidden.T, np.c_[xx.ravel(), yy.ravel()].T |
| 10. ) |
| 11. hiddenLayer_activations = sigmoid(hiddenLayer_linearTransform) |
| 12. outputLayer_linearTransform = np.dot(weights_hidden_output.T, hiddenLayer_activations) |
| 13. output_span = sigmoid(outputLayer_linearTransform) |
| 14. |
| 15. # Make predictions across region of interest |
| 16. labels = (output_span > 0.5).astype(int) |
| 17. |
| 18. # Plot decision boundary in region of interest |
| 19. z = labels.reshape(xx.shape) |
| 20. fig, ax = plt.subplots() |
| 21. ax.contourf(xx, yy, z, alpha=0.2) |
| 22. |
| 23. # Get predicted labels on training data and plot |
| 24. train_labels = (output > 0.5).astype(int) |
| 25. |
| 26. # create scatter plot |
| 27. ax.scatter(X[0, :], X[1, :], s=10, c=y.squeeze()) |
که همچین خروجی را می دهد
که همچنین به ما امکان می دهد بدانیم که شبکه عصبی ما چقدر در تلاش برای یافتن الگو در داده ها و سپس طبقه بندی آنها بر اساس آن مهارت دارد.
در قسمت زیر تمرینی برای شما قرار داده ایم – سعی کنید همان پیاده سازی را انجام دهید و با استفاده از scikit-learn روی مجموعه داده “blobs” پیاده سازی کنید. داده ها شبیه به تصویر زیر خواهند بود.
[اختیاری] دیدگاه ریاضی الگوریتم انتشار رو به عقب
Wi را وزن بین لایه ورودی و لایه پنهان و Wh را وزن بین لایه پنهان و لایه خروجی در نظر بگیرید. چقدر باشد
حال، h=σ (u)= σ (WiX)، یعنی h تابعی از u و u تابعی از Wi و X است. در اینجا ما تابع خود را به صورت σ نشان می دهیم.
Y= σ (u’)= σ (Whh)، یعنی Y تابعی از u’ و u’ تابعی از Wh و h است.
برای محاسبه مشتقات جزئی به طور مداوم به معادلات فوق ارجاع خواهیم کرد.
ما در درجه اول علاقه مند به یافتن دو عبارت ∂E/∂Wiو ∂E/∂Wh هستیم، یعنی تغییر در خطا در تغییر وزن بین لایه ورودی و لایه پنهان و تغییر در خطا در تغییر وزن بین لایه پنهان و لایه خروجی.
اما برای محاسبه هر دو مشتق جزئی، باید از قانون زنجیره ای تمایز جزئی استفاده کنیم زیرا E تابعی از Y و Y تابعی از u’ و u’ تابعی از Wi است.
بیایید از این ویژگی به خوبی استفاده کنیم و گرادیان ها را محاسبه کنیم.
∂E/∂Wh = (∂E/∂Y).( ∂Y/∂u’).( ∂u’/∂Wh), ……..(1)
می دانیم E به شکل E=(Y-t)2/2 است.
بنابراین، (∂E/∂Y)= (Y-t) می باشد.
حال، σ یک تابع سیگموئید است و دارای یک تمایز جالب از شکل σ(1- σ) است. من از خوانندگان می خواهم که این موضوع را برای خود بررسی کنند.
بنابراین، (∂Y/∂u’)= ∂( σ(u’)/ ∂u’= σ(u’)(1- σ(u’)).
اما، σ(u’)=Y، بنابراین،
(∂Y/∂u’)=Y(1-Y)
اکنون ( ∂u’/∂Wh)= ∂( Whh)/ ∂Wh = h
را با جایگزینی مقادیر معادله (1) دریافت می کنیم،
∂E/∂Wh = (Y-t). Y(1-Y).h
بنابراین، اکنون گرادیان بین لایه پنهان و لایه خروجی را محاسبه کرده ایم، وقت آن است که گرادیان بین لایه ورودی و لایه پنهان را محاسبه کنیم.
∂E/∂Wi =(∂ E/∂ h). (∂h/∂u).( ∂u/∂Wi)
اما، (∂ E/∂ h) = (∂E/∂Y).( ∂Y/∂u’).( ∂u’/∂h). با جایگزینی این مقدار در معادله فوق، نتیجه زیر را دریافت می کنیم،
∂E/∂Wi =[(∂E/∂Y).( ∂Y/∂u’).( ∂u’/∂h)]. (∂h/∂u).( ∂u/∂Wi)……………(2)
بنابراین، ابتدا محاسبه گرادیان بین لایه پنهان و لایه خروجی چه فایده ای داشت؟ همان طور که در رابطه (2) می بینید، ما قبلا ∂E/∂Y و ∂Y/∂u’ را محاسبه کرده ایم و در فضا و زمان محاسبات صرفه جویی می کنیم. پس از مدتی متوجه خواهیم شد که چرا این الگوریتم را الگوریتم انتشار به عقب می نامند.
بیایید مشتقات مجهول را در رابطه (2) محاسبه کنیم.
∂u’/∂h = ∂(Whh)/ ∂h = Wh
∂h/∂u = ∂( σ(u)/ ∂u= σ(u)(1- σ(u))
اما، σ(u)=h، بنابراین،
(∂Y/∂u)=h(1-h)
اکنون، ∂u/∂Wi = ∂(WiX)/ ∂Wi = X
با جایگزینی همه این مقادیر در رابطه (2) دریافت می کنیم:
∂E/∂Wi = [(Y-t). Y(1-Y).Wh].h(1-h).X
بنابراین، اکنون از آن جایی که ما هر دو گرادیان را محاسبه کرده ایم، وزن ها را می توان به عنوان زیر به روز کرد
Wh = Wh + η . ∂E/∂Wh
Wi = Wi + η . ∂E/∂Wi
که در آن η نرخ یادگیری است.
بنابراین به این سوال برمی گردیم: چرا این الگوریتم را الگوریتم انتشار به عقب می نامند؟
دلیل آن این است: اگر شکل نهایی ∂E/∂Wh و ∂E/∂Wi را مشاهده کردید، عبارت (Y-t) را که به معنی خطای خروجی می باشد، خواهید دید، که همان چیزی است که ما با آن شروع کردیم و سپس آن را به لایه ورودی، برای به روز رسانی وزن پس انتشار کردیم. بنابراین، این ریاضیات در کجای کد قرار می گیرد؟
hiddenlayer_activations=h (فعال سازی ها یا راه اندازی های لایه پنهانی)
E= Y-t
Slope_output_layer = Y(1-Y) (شیب لایه خروجی)
lr = η
slope_hidden_layer = h(1-h) (شیب لایه پنهان)
wout = Wh
اکنون به راحتی می توانید کد را با ریاضیات مرتبط کنید./

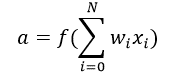






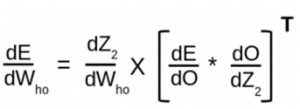
دیدگاهتان را بنویسید