یادگیری عمیق 2 - آکادمی علم داده نویان

به قسمت 2 در آموزش جامع یادگیری عمیق خوش آمدید.

در بخش اول مباحث زیر را مورد بحث قرار داده بودیم:

درباره یادگیری عمیق
وارد کردن مجموعه داده ها و بررسی اجمالی داده ها
گراف محاسباتی
اولیه سازی وزن ها و پارامتر ها
پیش انتشار
گرادیان نزول
پس نمایی استدلالی (Logistic Regression) با استفاده از Sklearn

در این مقاله به بحث ادامه داده و شبکه های عصبی مصنوعی (ANN) را معرفی خواهیم کرد.

محتویات

۱. شبکه های عصبی مصنوعی

یک شبکه عصبی به چه معناست؟
چند لایه مورد نیاز است تا یک شبکه عصبی «عمیق» نامیده شود؟
چرا لایه ها را پنهان می نامند؟

شبکه عصبی 2 لایه ای

ایجاد لایه ها و اولیه سازی وزن پارامتر ها و سوگیری ها
پیش انتشار
تابع هزینه و تابع ضرر
پس انتشار (Back Propagation)
به روزرسانی پارامتر ها
پیش بینی
ایجاد مدل

شبکه عصبی مصنوعی یا Artificial Neural Network (ANN)

نام دیگری برای شبکه عصبی عمیق یا یادگیری عمیق می باشد.

یک شبکه عصبی به چه معناست؟

شبکه عصبی در اصل به این معنی است این است که ما رگرسیون لوژستیکی را می گیریم و چندین بار آن را تکرار می کنیم. در یک رگرسیون لوژستیکی معمولی، یک لایه ورودی و یک لایه خروجی داریم. اما در مورد یک شبکه عصبی، حداقل یک لایه رگرسیون پنهان بین این لایه های ورودی و خروجی وجود دارد.

چند لایه مورد نیاز است تا یک شبکه عصبی «عمیق» نامیده شود؟

البته که هیچ مقدار خاصی از لایه ها برای طبقه بندی یک شبکه عصبی به عنوان شبکه عصبی عمیق وجود ندارد. اصطلاح «عمیق» صراحتا منسوب به هر مشکلی است. سوال درستی که می توانیم بپرسیم، سوال «چقدر عمیق؟» می باشد. به عنوان مثال سوال «استخر شنای شما چقدر عمیق است؟» را می توان به چند روش پاسخ داد. عمق آن می تواند ۲ متر یا ۱۰ متر باشد، اما دارای «عمق» است. همین طور شبکه عصبی ما، می تواند ۲ لایه پنهان یا «هزاران» لایه پنهان داشته باشد.

بنابراین در این مقاله بیشتر در مورد سوال “چقدر عمیق؟” تمرکز خواهیم کرد.

چرا لایه ها را پنهان می نامند؟

لایه ها را پنهان می نامند زیرا ورودی های اصلی (مجموعه آموزش) را نمی بینند. به عنوان مثال، فرض کنید شما شما یک NN با یک لایه ورودی، یک لایه پنهان، و یک لایه خروجی داشته باشد. وقتی از شما پرسیده شد که NN شما چند لایه دارد، پاسخ شما باید «۲ لایه دارد» باشد، زیرا هنگام محاسبات اولیه، یا لایه ورودی نادیده گرفته می شود.

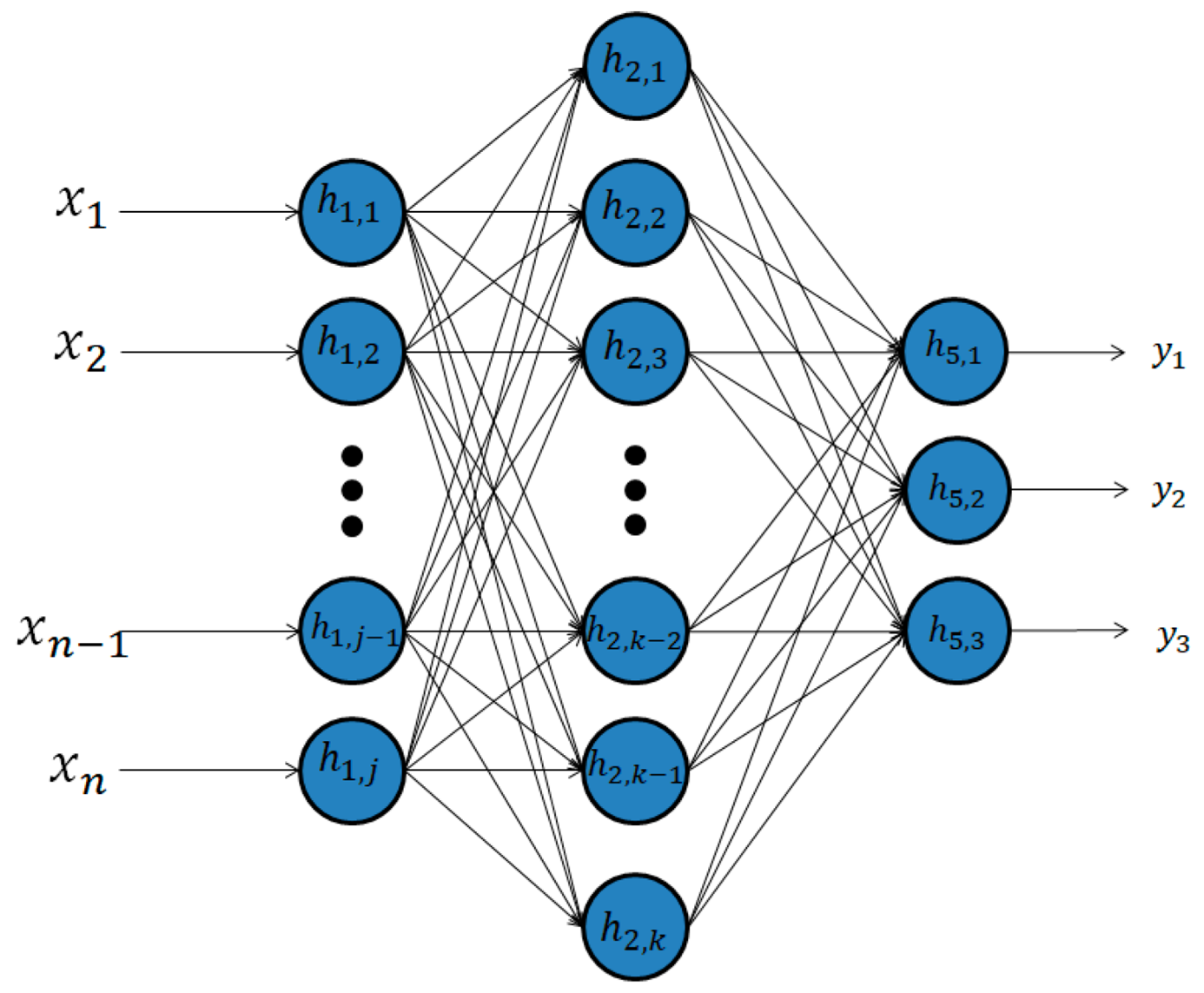
با کمک تصویر زیر می توانید یک شبکه عصبی 2 لایه ای را تجسم کنید:

منبع تصویر

گام به گام این تصویر را درک خواهیم کرد.

همان طور که می بینید در اینجا ما یک شبکه عصبی مصنوعی 2 لایه داریم. یک شبکه عصبی برای تقلید از نورون بیولوژیکی مغز انسان ایجاد شد. در ANN ما تعداد “k” عدد گره داریم. تعداد گره ها یک فراپارامتر است، که اساسا به این معنی است که مقدار آن توسط متخصص سازنده مدل پیکر بندی می شود.
لایه های ورودی و خروجی تغییر نمی کنند. ما ویژگی های ورودی “n” و 3 نتیجه ممکن داریم.
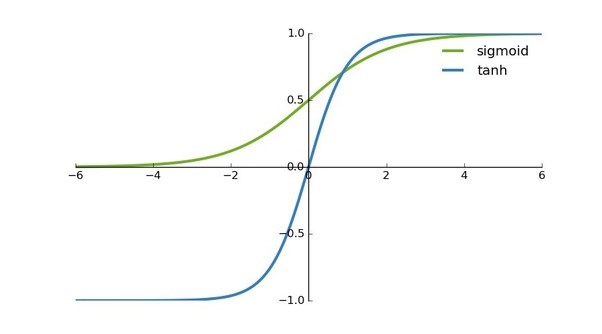
برخلاف رگرسیون لوژیستیک، شبکه های عصبی به جای تابع سیگموئید که کاملا با آن آشنا هستید، از تابع “tanh” به عنوان تابع فعال سازی خود استفاده می کنند. دلیل آن این است که میانگین خروجی آن به 0 نزدیک تر است که باعث می شود برای ورودی لایه بعدی متمرکز تر شود. تابع tanh می تواند باعث افزایش غیر خطی بودن مدل ما شود که باعث می شود مدل ما بهتر یاد بگیرد.

در رگرسیون لوژیستیک نرمال: ورودی Ü خروجی می باشد.

در حالی که در شبکه عصبی: ورودی Ü لایه پنهان Ü خروجی. لایه پنهان را می توان به عنوان خروجی قسمت 1 و ورودی قسمت 2 ANN ما تصور کرد. اکنون یک رویکرد کاربردی تر برای شبکه عصبی دو لایه خواهیم داشت.

(توجه مهم: این مقاله ادامه قسمت 1 خواهد بود تا از بارگذاری مجدد مجموعه داده و آماده کردن آن جلو گیری شود.)

شبکه عصبی 2 لایه ای

ایجاد لایه ها و مقدار دهی اولیه وزن پارامترها و سوگیری ها

مجموعه آموزشی ما 348 نمونه دارد، بنابراین x⁽³⁴⁸⁾. در رگرسیون لوژیستیک، سوگیری را در 0 و وزن ها را در 0.01 مقدار دهی کردیم. اما این بار وزن‌ ها را به‌ طور تصادفی مقدار دهی اولیه می‌کنیم، زیرا اگر آن ها را با 0 مقداردهی اولیه کنیم، تمام نورون‌ های لایه اول همان چیز هایی را محاسبه می‌کنند که نورون‌ های دیگر محاسبه می کنند. بنابراین به صورت تصادفی مقدار دهی اولیه می کنیم. همچنین، این وزن ‌های اولیه باید کوچک باشند، زیرا اگر در ابتدا بزرگ باشند، ورودی ‌ها را بزرگ می‌کنند و باعث می‌شوند که گرادیان ‌ها نزدیک به صفر باشند و الگوریتم بهینه ‌سازی را کند می‌کند.

سوگیری ها را می توان در ابتدا 0 کرد.

# intialize parameters and layer sizes

def initialize_parameters_and_layer_sizes_NN(x_train, y_train):

parameters = {“weight1”: np.random.randn(3,x_train.shape[0]) * 0.1,

“bias1”: np.zeros((3,1)),

“weight2”: np.random.randn(y_train.shape[0],3) * 0.1,

“bias2”: np.zeros((y_train.shape[0],1))}

return parameters

پیش انتشار

پیش انتشار تقریبا همان چیزی است که در رگرسیون لوژیستیک استفاده کردیم. تنها تفاوت در اینجا این است که از تابع tanh استفاده می کنیم و همه فرآیند ها را دو بار انجام می دهیم. تابع tanh در ماژول Numpy”” گنجانده شده است.

def forward_propagation_NN(x_train, parameters):

Z1 = np.dot(parameters[“weight1”],x_train) +parameters[“bias1”]

A1 = np.tanh(Z1)

Z2 = np.dot(parameters[“weight2”],A1) + parameters[“bias2”]

A2 = sigmoid(Z2)

cache = {“Z1”: Z1,

“A1”: A1,

“Z2”: Z2,

“A2”: A2

{

return A2, cache

تابع هزینه و تابع ضرر

توابع ضرر و هزینه همانند رگرسیون لوژیستیک است.

خطای آنتروپی متقاطع:

# Compute cost

def compute_cost_NN(A2, Y, parameters):

logprobs = np.multiply(np.log(A2),Y)

cost = -np.sum(logprobs)/Y.shape[1]

return cost

پس انتشار

پس انتشار اساسا مشتق است. این یک موضوع بسیار گسترده و حیاتی است که شایسته یک مقاله مختص این موضوع است. بیایید کد را بنویسیم:

# Backward Propagation

def backward_propagation_NN(parameters, cache, X, Y):

dZ2 = cache[“A2”]-Y

dW2 = np.dot(dZ2,cache[“A1”].T)/X.shape[1]

db2 = np.sum(dZ2,axis =1,keepdims=True)/X.shape[1]

dZ1 = np.dot(parameters[“weight2”].T,dZ2)*(1 – np.power(cache[“A1”], 2))

dW1 = np.dot(dZ1,X.T)/X.shape[1]

db1 = np.sum(dZ1,axis =1,keepdims=True)/X.shape[1]

grads = {“dweight1”: dW1,

“dbias1”: db1,

“dweight2”: dW2,

“dbias2”: db2}

return grads

به روز رسانی پارامتر ها

به روز رسانی پارامتر ها نیز مانند رگرسیون لوژیستیک است. به همین دلیل است که شما باید قسمت اول این مقاله را بخوانید. ما چندین بار از رگرسیون لوژیستیک استفاده خواهیم کرد زیرا بلوک سازنده یک شبکه عصبی مصنوعی می باشد.

# update parameters

def update_parameters_NN(parameters, grads, learning_rate = 0.01):

parameters = {“weight1”: parameters[“weight1”]-learning_rate*grads[“dweight1”],

“bias1”: parameters[“bias1”]-learning_rate*grads[“dbias1”],

“weight2”: parameters[“weight2”]-learning_rate*grads[“dweight2”],

“bias2”: parameters[“bias2”]-learning_rate*grads[“dbias2”]}

return parameters

پیش بینی

حال ما یک تابع برای پیش بینی درست می کنیم:

# prediction

def predict_NN(parameters,x_test):

# x_test is a input for forward propagation

A2, cache = forward_propagation_NN(x_test,parameters)

Y_prediction = np.zeros((1,x_test.shape[1]))

# if z is bigger than 0.5, our prediction is sign one (y_head=1),

# if z is smaller than 0.5, our prediction is sign zero (y_head=0),

for i in range(A2.shape[1]):

if A2[0,i]<= 0.5:

Y_prediction[0,i] = 0

else:

Y_prediction[0,i] = 1

return Y_prediction

ایجاد مدل

اکنون زمان آن است که همه این ها را کنار هم بگذاریم و جادو که اتفاق می افتد را ببینیم:

# 2 – Layer neural network

def two_layer_neural_network(x_train, y_train,x_test,y_test, num_iterations):

cost_list = []

index_list = []

#initialize parameters and layer sizes

parameters = initialize_parameters_and_layer_sizes_NN(x_train, y_train)

for i in range(0, num_iterations):

# forward propagation

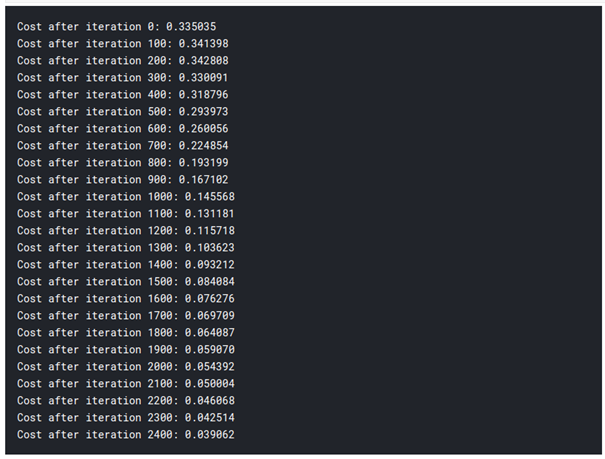
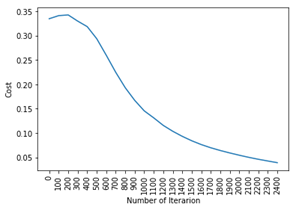
در مقاله قبلی، پس از استفاده از رگرسیون لوژیستیک، دقت 92% داشتیم. بنابراین می توانید ببینید که ما فقط با افزودن یک لایه اضافی از رگرسیون لوژیستیک، دقت بسیار بالاتری داریم. به همین دلیل است که شبکه‌ های عصبی یکی از فناوری ‌های روز دنیا هستند.