یادگیری بدون نظارت 3
10 الگوریتم خوشه بندی با پایتون
خوشه بندی یا تجزیه و تحلیل خوشه ای یک مشکل یادگیری بدون نظارت است.
اغلب به عنوان یک تکنیک تجزیه و تحلیل داده برای کشف الگو های جالب در داده ها، مانند گروه هایی از مشتریان بر اساس رفتار آنها، استفاده می شود.
الگوریتم های خوشه بندی زیادی برای انتخاب وجود دارد و بهترین الگوریتم خوشه بندی برای همه موارد وجود ندارد. در عوض، ایده خوبی است که طیف وسیعی از الگوریتم های خوشه بندی و پیکر بندی های مختلف را برای هر الگوریتم بررسی کنید.
در این آموزش، نحوه تطبیق و استفاده از الگوریتم های خوشه بندی برتر در پایتون را خواهید فهمید.
پس از تکمیل این آموزش، خواهید دانست:
- خوشه بندی یک مشکل بدون نظارت برای یافتن گروه های طبیعی در فضای ویژگی داده های ورودی است.
- بسیاری از الگوریتم های خوشه بندی مختلف وجود دارد و بهترین روش واحد برای همه مجموعه داده ها وجود ندارد.
- نحوه پیاده سازی، تناسب و استفاده از الگوریتم های خوشه بندی برتر در پایتون با کتابخانه یادگیری ماشینی scikit-learn.
پروژه خود را با کتاب جدید من تسلط بر یادگیری ماشین با پایتون، شامل آموزش های گام به گام و فایل های کد منبع پایتون برای همه نمونه ها، شروع کنید.
بیایید شروع کنیم.
مرور کلی آموزش
این آموزش به سه بخش تقسیم می شود؛ که عبارتند از:
- خوشه بندی
- الگوریتم های خوشه بندی
- نمونه هایی از الگوریتم های خوشه بندی
- نصب کتابخانه
- مجموعه داده های خوشه بندی
- انتشار میل
- خوشه بندی تجمعی
- BIRCH
- DBSCAN
- K-میانگین
- مینی-دسته K-میانگین
- میانگین انتقال
- OPTICS
- خوشه بندی طیفی
- حالت مخلوط گاوسی
خوشه بندی
تجزیه و تحلیل خوشه ای یا خوشه بندی یک وظیفه یادگیری ماشینی بدون نظارت است.
این شامل کشف خودکار گروه بندی طبیعی در داده ها است. بر خلاف یادگیری نظارت شده (مانند مدل سازی پیش بینی)، الگوریتم های خوشه بندی فقط داده های ورودی را تفسیر می کنند و گروه ها یا خوشه های طبیعی را در فضای ویژگی پیدا می کنند.
Ü تکنیک های خوشه بندی زمانی اعمال می شوند که کلاسی برای پیش بینی وجود نداشته باشد، بلکه زمانی که نمونه ها باید به گروه های طبیعی تقسیم شوند، اعمال می شوند.
— صفحه 141، داده کاوی: ابزار ها و تکنیک های یادگیری ماشین عملی، 2016.
خوشه اغلب ناحیهای از چگالی در فضای ویژگی است که در آن نمونه هایی از دامنه (مشاهدات یا ردیف هایی از داده ها) نسبت به خوشه های دیگر به خوشه نزدیک تر هستند. خوشه ممکن است دارای یک مرکز (مرکز) باشد که یک نمونه یا یک فضای ویژگی نقطه ای است و ممکن است یک مرز یا وسعت داشته باشد.
Ü این خوشه ها احتمالا مکانیسمی را در حوزه ای که نمونه ها از آن ترسیم می شوند منعکس می کنند، مکانیزمی که باعث می شود برخی از نمونه ها شباهت بیشتری به یکدیگر داشته باشند تا نمونه های باقی مانده.
— صفحات 141 142، داده کاوی: ابزارها و تکنیک های یادگیری ماشین عملی، 2016.
خوشه بندی می تواند به عنوان یک فعالیت تجزیه و تحلیل داده ها به منظور کسب اطلاعات بیشتر در مورد حوزه مشکل، به اصطلاح کشف الگو یا کشف دانش مفید باشد.
مثلا:
- درخت تبارزایی (Phylogenetic tree) را می توان نتیجه تجزیه و تحلیل خوشه بندی دستی در نظر گرفت.
- جداسازی داده های معمولی از نقاط پرت یا ناهنجاری ممکن است یک مشکل خوشه بندی در نظر گرفته شود.
- جداسازی خوشه ها بر اساس رفتار طبیعی آنها یک مشکل خوشه بندی است که به آن تقسیم بندی بازار می گویند.
خوشه بندی همچنین می تواند به عنوان یک نوع مهندسی ویژگی مفید باشد، که در آن نمونه های موجود و جدید می توانند نگاشت شوند و به عنوان متعلق به یکی از خوشه های شناسایی شده در داده ها برچسب گذاری شوند.
ارزیابی خوشه های شناسایی شده ذهنی است و ممکن است به یک متخصص حوزه نیاز داشته باشد، اگرچه بسیاری از معیار های کمی خاص خوشه بندی وجود دارد. به طور معمول، الگوریتم های خوشه بندی به صورت آکادمیک بر روی مجموعه داده های مصنوعی با خوشه های از پیش تعریف شده مقایسه می شوند، که انتظار می رود الگوریتم آنها را کشف کند.
- خوشه بندی یک تکنیک یادگیری بدون نظارت است، بنابراین ارزیابی کیفیت خروجی هر روشی دشوار است.
– صفحه 534، یادگیری ماشینی: یک دیدگاه احتمالی، 2012.
الگوریتم های خوشه بندی
انواع مختلفی از الگوریتم های خوشه بندی وجود دارد.
بسیاری از الگوریتم ها از شباهت یا اندازهگیری فاصله بین نمونه ها در فضای ویژگی در تلاش برای کشف مناطق متراکم مشاهدات استفاده می کنند. به این ترتیب، اغلب تمرین خوبی است که داده ها را قبل از استفاده از الگوریتم های خوشه بندی مقیاس بندی کنید.
- محور همه اهداف تجزیه و تحلیل خوشه ای، مفهوم درجه شباهت (یا عدم تشابه) بین اشیاء منفرد در حال خوشه بندی است. یک روش خوشه بندی تلاش می کند تا اشیاء را بر اساس تعریف شباهت ارائه شده به آن گروه بندی کند.
– صفحه 502، عناصر یادگیری آماری: داده کاوی، استنتاج و پیش بینی، 2016.
برخی از الگوریتم های خوشه بندی از شما می خواهند که تعداد خوشه هایی را برای کشف در داده ها مشخص یا حدس بزنید، در حالی که برخی دیگر نیاز به مشخص کردن حداقل فاصله بین مشاهدات دارند که در آن نمونه ها ممکن است «نزدیک» یا «متصل» در نظر گرفته شوند.
به این ترتیب، تجزیه و تحلیل خوشهای یک فرآیند تکراری است که در آن ارزیابی ذهنی خوشههای شناسایی شده به تغییرات در پیکربندی الگوریتم بازخورد داده می شود تا زمانی که یک نتیجه مطلوب یا مناسب به دست آید.
کتابخانه scikit-learn مجموعه ای از الگوریتم های خوشه بندی مختلف را برای انتخاب فراهم می کند.
لیستی از 10 الگوریتم محبوب تر به شرح زیر است:
- انتشار میل
- خوشه بندی تجمعی
- BIRCH
- DBSCAN
- K-میانگین
- مینی-دسته K-میانگین
- میانگین انتقال
- OPTICS
- خوشه بندی طیفی
- مخلوطی از گاوسیان (Mixture of Gaussians)
هر الگوریتم رویکرد متفاوتی را برای چالش کشف گروه های طبیعی در داده ها ارائه می دهد.
به هیچ وجه بهترین الگوریتم خوشه بندی وجود ندارد و هیچ راه آسانی برای یافتن بهترین الگوریتم برای داده های خود بدون استفاده از آزمایش های کنترل شده وجود ندارد.
در این آموزش، نحوه استفاده از هر یک از این 10 الگوریتم خوشه بندی محبوب را از کتابخانه scikit-learn مرور خواهیم کرد.
مثال ها مبنایی را برای شما فراهم می کنند تا نمونه ها را کپی کنید و روش ها را روی داده های خود آزمایش کنید.
ما به تئوری مربوط به نحوه عملکرد الگوریتم ها یا مقایسه مستقیم آنها نخواهیم پرداخت. برای شروع در مورد این موضوع، به Clustering, scikit-learn API نگاهی بیندازید.
نمونه هایی از الگوریتم های خوشه بندی
در این بخش، نحوه استفاده از 10 الگوریتم خوشه بندی محبوب در scikit-learn را بررسی خواهیم کرد.
این شامل مثالی از برازش مدل و مثالی از تجسم نتیجه است.
نمونه ها برای شما طراحی شده اند تا بتوانید در پروژه خود کپی پیست کنید و روش ها را روی داده های خود اعمال کنید.
نصب کتابخانه
ابتدا بیایید کتابخانه را نصب کنیم.
این مرحله را نادیده نگیرید زیرا باید مطمئن شوید که آخرین نسخه را نصب کرده اید.
می توانید کتابخانه scikit-learn را با استفاده از نصب کننده pip پایتون به شرح زیر نصب کنید:
|
sudo pip install scikit-learn |
برای دستورالعمل های نصب اضافی مخصوص پلتفرم خود، نصب scikit Learn را
ببینید.
در مرحله بعد، اطمینان حاصل کنید که کتابخانه نصب شده است و شما از یک نسخه مدرن استفاده می کنید.
اسکریپت زیر را برای چاپ شماره نسخه کتابخانه اجرا کنید.
|
1 2 3 |
# check scikit-learn version import sklearn print(sklearn.__version__) |
با اجرای مثال، باید شماره نسخه زیر یا بالاتر را ببینید.
0.22.1
خوشه بندی مجموعه داده ها
ما از تابع ()make_classification برای ایجاد یک مجموعه داده طبقه بندی باینری آزمایشی استفاده خواهیم کرد.
مجموعه داده دارای 1000 نمونه با دو ویژگی ورودی و یک خوشه در هر کلاس خواهد بود. خوشه ها از نظر بصری در دو بعد مشخص هستند تا بتوانیم داده ها را با نمودار پراکنده رسم کنیم و نقاط موجود در نمودار را توسط خوشه اختصاص داده شده رنگ آمیزی کنیم. این کار کمک خواهد کرد که حداقل در مسئله آزمون، میزان “خوب” خوشه ها شناسایی شوند.
خوشه ها در این مسئله آزمایشی مبتنی بر گاوسی چند متغیره هستند و همه الگوریتم های خوشه بندی در شناسایی این نوع خوشه ها مؤثر نیستند. به این ترتیب، نتایج این آموزش نباید به عنوان مبنایی برای مقایسه روش ها به طور کلی استفاده شود.
نمونه ای از ایجاد و خلاصه کردن خوشه بندی مجموعه داده های مصنوعی در زیر فهرست شده است.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# synthetic classification dataset from numpy import where from sklearn.datasets import make_classification from matplotlib import pyplot # define dataset X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # create scatter plot for samples from each class for class_value in range(2): # get row indexes for samples with this class row_ix = where(y == class_value) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
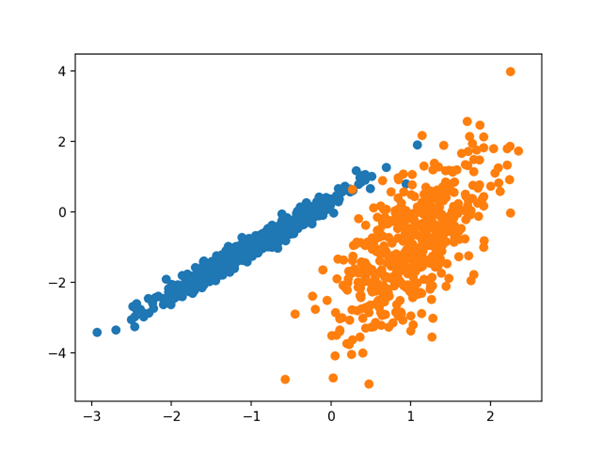
اجرای مثال خوشه بندی مجموعه داده مصنوعی را ایجاد می کند، سپس یک نمودار پراکنده از داده های ورودی با نقاط رنگ شده با برچسب کلاس (خوشه های ایده آل) ایجاد می کند.
ما به وضوح می توانیم دو گروه متمایز از داده ها را در دو بعد ببینیم و امیدواریم که یک الگوریتم خوشه بندی خودکار بتواند این گروه بندی ها را شناسایی کند.
طرح پراکندگی خوشه بندی مجموعه داده های مصنوعی با نقاط رنگ آمیزی شده توسط خوشه شناخته شده
در مرحله بعد، می توانیم نمونه هایی از الگوریتم های خوشه بندی اعمال شده در این مجموعه داده را شروع کنیم.
من چند تلاش حداقلی برای تنظیم هر روش با مجموعه داده انجام داده ام.
آیا می توانید برای یکی از الگوریتم ها نتیجه بهتری بگیرید؟
انتشار میل
انتشار میل شامل یافتن مجموعه ای از نمونه هایی است که داده ها را به بهترین شکل خلاصه می کند.
- ما روشی به نام “انتشار میل” ابداع کردیم، که به عنوان معیار های ورودی شباهت بین جفت نقاط داده را می گیرد. پیام های با ارزش واقعی بین نقاط داده رد و بدل می شوند تا زمانی که مجموعه ای با کیفیت بالا از نمونه ها و خوشه های مربوطه به تدریج پدیدار شوند.
– خوشه بندی با ارسال پیام بین نقاط داده، 2007.
این تکنیک در مقاله فوق توضیح داده شده است:
از طریق کلاس AffinityPropagation پیاده سازی می شود و پیکربندی اصلی برای تنظیم، تنظیم بین 0.5 و 1 و شاید «ترجیح» است.
نمونه کامل در زیر آمده است.
| 1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# affinity propagation clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AffinityPropagation from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = AffinityPropagation(damping=0.9) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
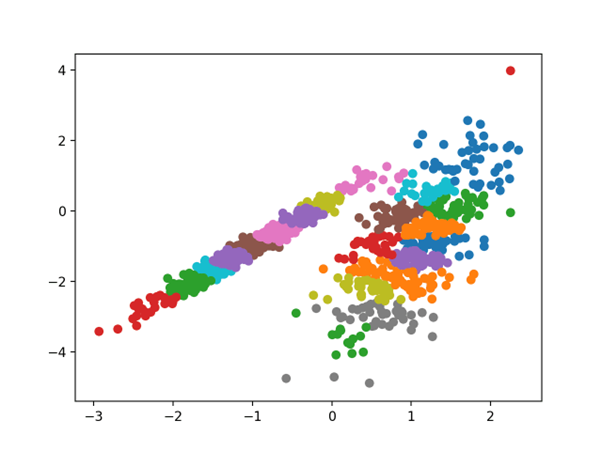
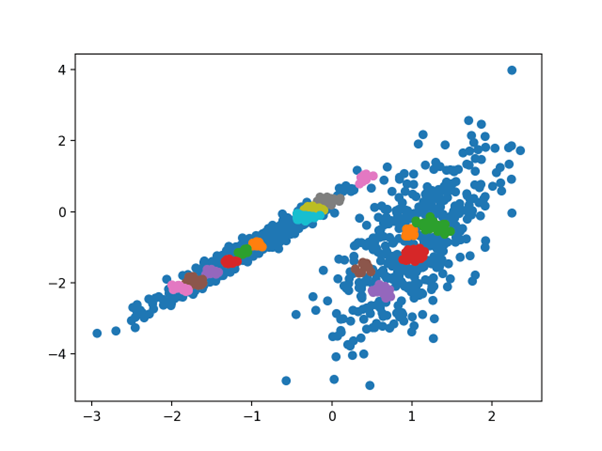
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این صورت نتوانستم به نتیجه خوبی برسم.
نمودار پراکندگی مجموعه داده با خوشه های شناسایی شده با استفاده از انتشار میل
خوشه بندی تجمعی
خوشه بندی تجمعی شامل ادغام نمونه ها تا رسیدن به تعداد مطلوب خوشه است.
این بخشی از یک کلاس گسترده تر از روش های خوشه بندی سلسله مراتبی است و می توانید در اینجا اطلاعات بیشتری کسب کنید:
از طریق کلاس AgglomerativeClustering پیاده سازی می شود و پیکربندی اصلی برای تنظیم مجموعه “n_clusters” است، تخمینی از تعداد خوشه ها در داده ها، به عنوان مثال؛2.
نمونه کامل در زیر آمده است.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# agglomerative clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AgglomerativeClustering from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = AgglomerativeClustering(n_clusters=2) # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
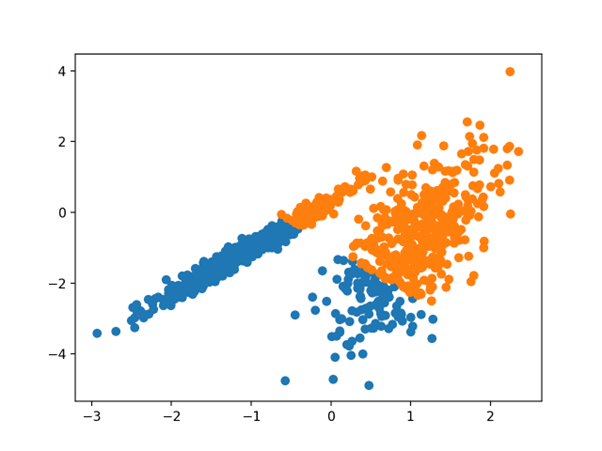
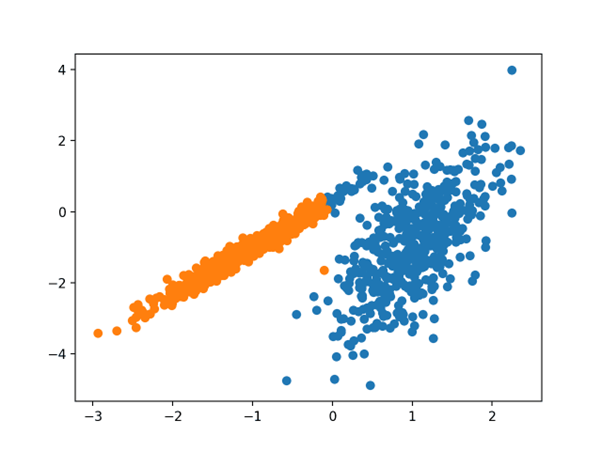
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این صورت یک گروه بندی معقول پیدا می شود.
نمودار پراکندگی مجموعه داده با خوشه های شناسایی شده با استفاده از خوشه بندی تجمعی
BIRCH
خوشه بندی BIRCH (BIRCH مخفف عبارت Balanced Iterative Reducing and Clustering using Hierarchies) می باشد و شامل ساختن یک ساختار درختی است که مرکز های خوشه ای از آن استخراج می شوند.
- BIRCH به صورت فزاینده و پویا نقاط داده های متریک چند بعدی دریافتی را خوشه بندی می کند تا سعی کند با منابع موجود (به عنوان مثال، محدودیت های حافظه و زمانی در دسترس) بهترین خوشه بندی را با کیفیت تولید کند.
– BIRCH: یک روش خوشه بندی داده کارآمد برای پایگاه های داده بزرگ، 1996.
این تکنیک در مقاله فوق توضیح داده شده است:
از طریق کلاس Birch پیاده سازی می شود و پیکربندی اصلی برای تنظیم فراپارامتر های “آستانه” و “n_cluster” است که مورد آخر تخمینی از تعداد خوشه ها را ارائه می کند.
نمونه کامل در زیر آمده است.
|
# birch clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import Birch from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = Birch(threshold=0.01, n_clusters=2) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
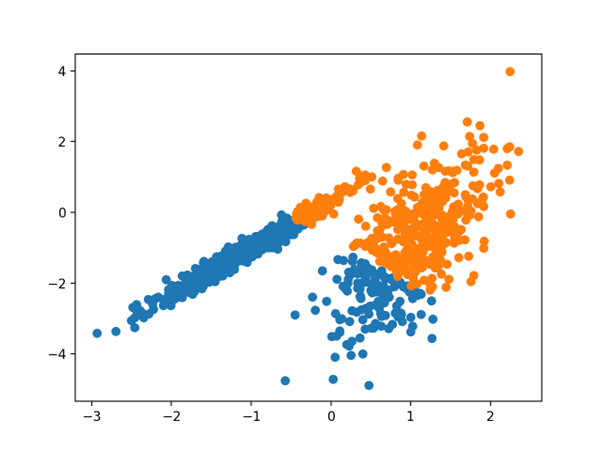
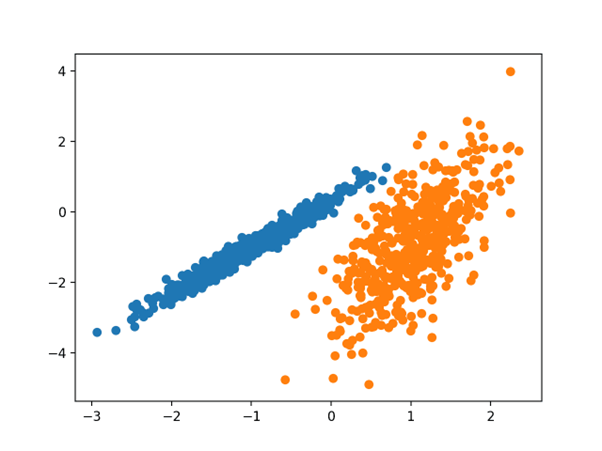
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این مورد، یک گروه بندی عالی پیدا می شود.
نمودار پراکندگی مجموعه داده با خوشه های شناسایی شده با استفاده از خوشه بندی BIRCH
DBSCAN
خوشه بندی DBSCAN (که در آن DBSCAN مخفف عبارت Density Spatial Clustering of Applications with Noise است) شامل یافتن نواحی با چگالی بالا در دامنه و گسترش آن نواحی از فضای ویژگی اطراف آنها به عنوان خوشه است.
- ما الگوریتم خوشه بندی جدید DBSCAN را با تکیه بر مفهومی مبتنی بر چگالی از خوشه ها ارائه می کنیم که برای کشف خوشه هایی با شکل دلخواه طراحی شده است. DBSCAN تنها به یک پارامتر ورودی نیاز دارد و از کاربر در تعیین مقدار مناسب برای آن پشتیبانی می کند
– الگوریتم مبتنی بر چگالی برای کشف خوشه ها در پایگاه های داده فضایی بزرگ با نویز، 1996.
این تکنیک در مقاله فوق توضیح داده شده است.
از طریق کلاس DBSCAN پیاده سازی می شود و پیکربندی اصلی برای تنظیم، هایپر پارامتر های “eps” و “min_samples” است.
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این مورد، یک گروه بندی معقول پیدا می شود، اگرچه تنظیم بیشتری لازم است.
K-میانگین
خوشه بندی K-میانگین ممکن است شناخته شده ترین الگوریتم خوشه بندی باشد و شامل اختصاص مثال هایی به خوشه ها در تلاش برای به حداقل رساندن واریانس در هر خوشه است.
- هدف اصلی این مقاله توصیف فرآیندی برای تقسیم یک جمعیت N بعدی به k مجموعه بر اساس یک نمونه است. به نظر میرسد این فرآیند، که «means-k » نامیده می شود، پارتیشن هایی را ارائه می دهد که از نظر واریانس درون کلاسی کارآمد هستند.
– چند روش برای طبقه بندی و تحلیل مشاهدات چند متغیره، 1967.
این تکنیک در ویکی پدیا خوشه بندی K-میانگین توضیح داده شده است.
از طریق کلاس K-Means پیاده سازی می شود و پیکربندی اصلی برای تنظیم، فراپارامتر «n_cluster» است که روی تعداد تخمینی خوشه ها در داده ها تنظیم شده است.
نمونه کامل در زیر آمده است.
| 1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# dbscan clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import DBSCAN from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = DBSCAN(eps=0.30, min_samples=9) # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این مورد، یک گروه بندی معقول پیدا می شود، اگرچه واریانس مساوی نابرابر در هر بعد، روش را برای این مجموعه داده مناسب تر می کند.
نمودار پراکندگی مجموعه داده با خوشه های شناسایی شده با استفاده از K-Means Clustering
مینی دسته K-میانگین
Mini-Batch K-Means یک نسخه اصلاح شده از k-میانگین است که با استفاده از دسته های کوچک نمونه ها به جای کل مجموعه داده، به روز رسانی به مرکز های خوشه ای را انجام می دهد، که می تواند آن را برای مجموعه داده های بزرگ سریعتر کند، و شاید برای نویز های آماری قوی تر عمل کند.
… ما استفاده از بهینه سازی دسته ای-کوچک را برای k-میانگین به معنای خوشه بندی پیشنهاد می کنیم. این هزینه محاسباتی را در مقایسه با الگوریتم دسته ای کلاسیک کاهش می دهد در حالی که راه حلهای بسیار بهتری نسبت به شیب نزولی تصادفی آنلاین ارائه می دهد.
— مقیاس-وب خوشه بندی K-میانگین ، 2010.
این تکنیک در مقاله فوق توضیح داده شده است.
از طریق کلاس Mini-Batch K-Means پیاده سازی می شود و پیکربندی اصلی برای تنظیم، هایپرپارامتر “n_cluster” است که بر روی تعداد تخمینی خوشه ها در داده ها تنظیم شده است.
نمونه کامل در زیر آمده است.
| 1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# mini-batch k-means clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MiniBatchKMeans from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = MiniBatchKMeans(n_clusters=2) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این حالت، نتیجه ای معادل الگوریتم k-میانگین استاندارد پیدا می شود.
نمودار پراکندگی مجموعه داده با خوشه های شناسایی شده با استفاده از دسته-کوچک خوشه بندی K-میانگین است
میانگین انتقال
خوشه بندی میانگین انتقال شامل یافتن و تطبیق مرکز ها بر اساس تراکم نمونه ها در فضای ویژگی است.
- ما برای داده های گسسته هم گرایی یک روش تغییر میانگین بازگشتی را به نزدیک ترین نقطه ثابت تابع چگالی زیرین و بنابراین کاربرد آن در تشخیص حالت های چگالی را ثابت می کنیم.
– میانگین انتقال: رویکردی قوی به سمت تحلیل فضای ویژگی، 2002.
این تکنیک در مقاله فوق توضیح داده شده است:
از طریق کلاس MeanShift پیاده سازی می شود و پیکربندی اصلی برای تنظیم، فراپارامتر “پهنای باند” است.
نمونه کامل در زیر آمده است.
| 1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# mean shift clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MeanShift from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = MeanShift() # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این مورد، مجموعه معقولی از خوشه ها در داده ها یافت می شود.
OPTICS
خوشه بندی OPTICS (که در آن OPTICS مخفف Ordering Points To Identify the Clustering Structure است) یک نسخه اصلاح شده از DBSCAN است که در بالا توضیح داده شد.
- ما الگوریتم جدیدی را به منظور تجزیه و تحلیل خوشه ای معرفی می کنیم که به طور صریح خوشه بندی یک مجموعه داده را تولید نمی کند. اما درعوض یک ترتیب افزوده از پایگاه داده ایجاد می کند که ساختار خوشه بندی مبتنی بر چگالی آن را نشان می دهد. این ترتیب خوشهای حاوی اطلاعاتی است که معادل خوشه بندی های مبتنی بر چگالی مربوط به طیف وسیعی از تنظیمات پارامتر است.
– OPTICS: ترتیب نقاط برای شناسایی ساختار خوشه بندی، 1999.
این تکنیک در مقاله فوق توضیح داده شده است.
از طریق کلاس OPTICS پیاده سازی می شود و پیکربندی اصلی برای تنظیم، هایپرپارامترهای “eps” و “min_samples” است.
نمونه کامل در زیر آمده است.
| 1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# optics clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import OPTICS from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = OPTICS(eps=0.8, min_samples=10) # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این مورد، من نتوانستم به یک نتیجه معقول در این مجموعه داده برسم.
نمودار پراکندگی مجموعه داده با خوشه های شناسایی شده با استفاده از خوشه بندی OPTICS
خوشه بندی طیفی
خوشه بندی طیفی یک دسته کلی از روش های خوشه بندی است که از جبر خطی استخراج می شود.
- یک جایگزین امیدوار کننده که اخیرا در تعدادی از زمینه ها ظهور کرده است، استفاده از روش های طیفی برای خوشه بندی است. در اینجا، یکی از بردار های ویژه بالای یک ماتریس به دست آمده از فاصله بین نقاط استفاده می کند.
– در مورد خوشه بندی طیفی: تجزیه و تحلیل و یک الگوریتم، 2002.
این تکنیک در مقاله بالا توضیح داده شده است.
از طریق کلاس SpectralClustering پیاده سازی می شود و خوشه بندی طیفی اصلی یک کلاس کلی از روش های خوشه بندی است که از جبر خطی گرفته شده است. برای تنظیم، هایپرپارامتر “n_cluster” است که برای تعیین تعداد تخمینی خوشه ها در داده ها استفاده می شود.
نمونه کامل در زیر آمده است.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# spectral clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import SpectralClustering from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = SpectralClustering(n_clusters=2) # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این مورد، خوشه های معقولی پیدا شد.
نمودار پراکندگی مجموعه داده با خوشه های شناسایی شده با استفاده از خوشه بندی طیفی
مدل مخلوط گاوسی
یک مدل مخلوط گاوسی یک تابع چگالی احتمال چند متغیره را با مخلوطی از توزیع های احتمال گاوسی خلاصه میکند که از نامش پیداست.
برای اطلاعات بیشتر در مورد مدل، نگاه کنید به:
از طریق کلاس GaussianMixture پیاده سازی می شود و پیکربندی اصلی برای تنظیم، هایپرپارامتر “n_clusters” است که برای تعیین تعداد تخمینی خوشه ها در داده ها استفاده می شود.
نمونه کامل در زیر آورده شده است.
|
# gaussian mixture clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.mixture import GaussianMixture from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = GaussianMixture(n_components=2) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show() |
اجرای مثال با مدل بر روی مجموعه داده آموزشی مطابقت دارد و برای هر نمونه در مجموعه داده یک خوشه پیش بینی می کند. سپس یک نمودار پراکندگی با نقاط رنگ آمیزی شده توسط خوشه اختصاص داده شده ایجاد می شود.
در این حالت می توان دید که خوشه ها کاملا شناسایی شدند. با توجه به اینکه مجموعه داده به عنوان مخلوطی از گاوسی ها تولید شده است، تعجب آور نیست.
نمودار پراکندگی مجموعه داده با خوشه های شناسایی شده با استفاده از خوشه بندی مخلوط گاوسی

دیدگاهتان را بنویسید