یادگیری بدون نظارت 2

5 الگوریتم خوشه بندی که دانشمندان داده باید بدانند

خوشه بندی یک تکنیک یادگیری ماشینی است که شامل گروه بندی نقاط داده است. با توجه به مجموعه ای از نقاط داده، می توانیم از یک الگوریتم خوشه بندی برای طبقه بندی هر نقطه داده در یک گروه خاص استفاده کنیم. در تئوری، نقاط داده ای که در یک گروه قرار دارند باید دارای مشخصات و / یا ویژگی های مشابه باشند، در حالی که نقاط داده در گروه های مختلف باید دارای مشخصات و / یا ویژگی های بسیار متفاوت باشند. خوشه بندی یک روش یادگیری بدون نظارت است و یک تکنیک رایج برای تجزیه و تحلیل داده های آماری است که در بسیاری از زمینه ها استفاده می شود.

در علم داده، ما می‌توانیم از تجزیه و تحلیل خوشه ‌بندی برای به دست آوردن بینش ‌های ارزشمند از داده‌ های خود با دیدن اینکه نقاط داده در هنگام اعمال الگوریتم خوشه ‌بندی در چه گروه‌ هایی قرار می ‌گیرند، استفاده کنیم. امروز، 5 الگوریتم خوشه ‌بندی محبوب را که دانشمندان داده باید بدانند و مزایا و معایب آنها را بررسی می ‌کنیم!

K-میانگین خوشه بندی

K-میانگین خوشه بندی احتمالا شناخته شده ترین الگوریتم خوشه بندی است. در بسیاری از کلاس های مقدماتی علم داده و یادگیری ماشین تدریس می شود. درک و پیاده سازی آن در کد آسان است! برای یک تصور، گرافیک زیر را بررسی کنید.

K-میانگین خوشه بندی

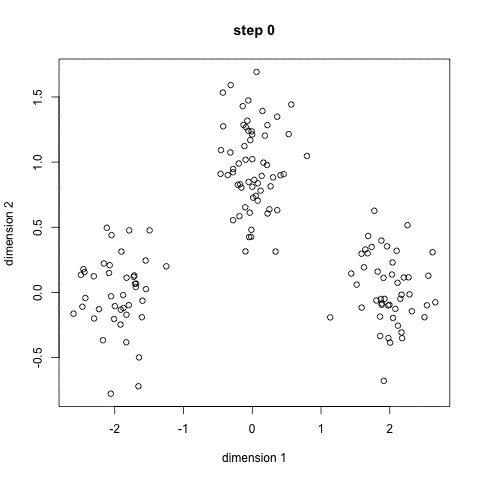
1. برای شروع، ابتدا تعدادی کلاس / گروه را برای استفاده انتخاب می کنیم و به طور تصادفی نقاط مرکزی مربوطه آنها را مقدار دهی اولیه می کنیم. برای تعیین تعداد کلاس‌ های مورد استفاده، بهتر است نگاهی گذرا به داده ‌ها بیندازید و سعی کنید گروه‌ های متمایز را شناسایی کنید. نقاط مرکزی بردار هایی با طول هر بردار نقطه داده هستند و در نمودار بالا “X” هستند.
2. هر نقطه داده با محاسبه فاصله بین آن نقطه و هر مرکز گروه طبقه بندی می شود و سپس نقطه در گروهی که مرکز آن نزدیک به آن است طبقه بندی می شود.
3. بر اساس این نکات طبقه بندی شده، مرکز گروه را با میانگین تمام بردار های گروه محاسبه می کنیم.
4. این مراحل را برای تعداد مشخصی از تکرار ها تکرار کنید یا تا زمانی که مراکز گروه بین تکرار ها تغییر زیادی نکنند. همچنین می‌ توانید چند بار به‌ طور تصادفی مراکز گروه را مقدار دهی اولیه کنید و سپس اجرایی را انتخاب کنید که به نظر می ‌رسد بهترین نتایج را ارائه می ‌دهد.

K-میانگین این مزیت را دارد که بسیار سریع است، زیرا تمام کاری که ما واقعا انجام می دهیم محاسبه فاصله بین نقاط و مراکز گروه است. با انجام محاسبات بسیار کم! بنابراین پیچیدگی خطی O(n) دارد.

از طرف دیگر، K-میانگین دارای چند معایب است. ابتدا باید انتخاب کنید که چند گروه / کلاس وجود دارد. این همیشه بی ‌اهمیت نیست و در حالت ایده‌ آل، با الگوریتم خوشه‌ بندی، می‌ خواهیم آن ‌ها را برای ما مشخص کند، زیرا هدف آن کسب بینش از داده ‌ها است. میانگین K نیز با انتخاب تصادفی مراکز خوشه شروع می شود و بنابراین ممکن است نتایج خوشه بندی متفاوتی در اجرا های مختلف الگوریتم به همراه داشته باشد. بنابراین، نتایج ممکن است تکرار پذیر نباشند و سازگاری نداشته باشند. سایر روش های خوشه ای سازگارتر هستند.

K -میانه (K-Medians) یکی دیگر از الگوریتم های خوشه بندی مربوط به K-میانگین است، به جز اینکه به جای محاسبه مجدد نقاط مرکز گروه با استفاده از میانگین، از بردار میانه گروه استفاده می کنیم. این روش حساسیت کمتری نسبت به نقاط پرت دارد (به دلیل استفاده از میانه) اما برای مجموعه داده های بزرگتر بسیار کند تر است زیرا هنگام محاسبه بردار میانه به مرتب سازی در هر تکرار نیاز است.

انتقال-میانگین خوشه بندی

خوشه بندی میانگین تغییر یک الگوریتم مبتنی بر پنجره کشویی است که تلاش می کند مناطق متراکم از نقاط داده را پیدا کند. این یک الگوریتم مبتنی بر مرکز است به این معنی که هدف، مکان یابی نقاط مرکزی هر گروه / کلاس است، که با به روز رسانی کاندید ها برای نقاط مرکزی به عنوان میانگین نقاط درون پنجره کشویی کار می کند. سپس این پنجره ‌های کاندید در مرحله پس پردازش فیلتر می‌ شوند تا موارد مشابه را حذف کنند و مجموعه نهایی نقاط مرکزی و گروه‌ های مربوطه را تشکیل دهند. برای یک تصور، گرافیک زیر را بررسی کنید.

انتقال-میانگین خوشه بندی برای یک پنجره کشویی

1. برای توضیح تغییر میانگین، مجموعه ای از نقاط را در فضای دو بعدی مانند تصویر بالا در نظر می گیریم. ما با یک پنجره کشویی دایره ای در مرکز نقطه C (به طور تصادفی انتخاب شده) و دارای شعاع r به عنوان هسته شروع می کنیم. میانگین-انتقال یک الگوریتم تپه-نوردی است که شامل جابجایی این هسته به صورت مکرر به ناحیه ای با تراکم بالاتر در هر پله تا زمان همگرایی است.
2. در هر تکرار، پنجره کشویی با جابجایی نقطه مرکزی به میانگین نقاط درون پنجره (از این رو به این نام است) به سمت مناطق با تراکم بالاتر منتقل می شود. چگالی درون پنجره کشویی متناسب با تعداد نقاط داخل آن است. طبیعتا با جابجایی به میانگین نقاط در پنجره به تدریج به سمت مناطق با تراکم نقطه بالاتر حرکت می کند.
3. ما به جابجایی پنجره کشویی مطابق با میانگین ادامه می دهیم تا جایی که هیچ جهتی وجود نداشته باشد که یک انتقال بتواند نقاط بیشتری را در داخل هسته جای دهد. گرافیک بالا را بررسی کنید؛ ما به حرکت دایره ادامه می دهیم تا زمانی که دیگر چگالی (یعنی تعداد نقاط در پنجره) را افزایش دهیم.
4. این فرآیند مراحل 1 تا 3 با بسیاری از پنجره های کشویی انجام می شود تا زمانی که همه نقاط در یک پنجره قرار گیرند. هنگامی که چندین پنجره کشویی روی هم قرار می گیرند، پنجره حاوی بیشترین نقاط حفظ می شود. سپس نقاط داده بر اساس پنجره کشویی که در آن قرار دارند، خوشه بندی می شوند.

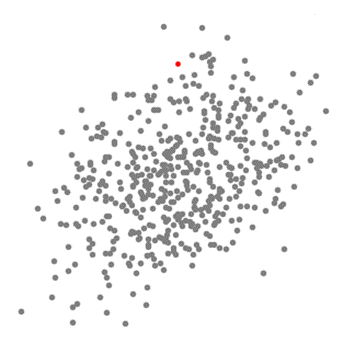
تصویری از کل فرآیند از انتهای تا انتها با تمام پنجره های کشویی در زیر نشان داده شده است. هر نقطه سیاه نمایانگر مرکز یک پنجره کشویی و هر نقطه خاکستری یک نقطه داده است.

کل فرآیند خوشه بندی میانگین-انتقال

در مقابل K-میانگین خوشه بندی، نیازی به انتخاب تعداد خوشه ها نیست زیرا تغییر میانگین به طور خودکار این موضوع را کشف می کند. این یک مزیت بزرگ است. این واقعیت که مراکز خوشه به سمت نقاط حداکثر چگالی همگرا می شوند نیز کاملا مطلوب است زیرا درک آن کاملا شهودی است و به خوبی در یک مفهوم مبتنی بر داده های طبیعی مطابقت دارد. اشکال این است که انتخاب اندازه  /  شعاع پنجره “r” می‌تواند بی ‌اهمیت باشد.

خوشه بندی فضایی مبتنی بر چگالی برنامه های کاربردی با نویز (DBSCAN)

DBSCAN یک الگوریتم خوشه ای مبتنی بر چگالی است که مشابه تغییر میانگین است، اما با چند مزیت قابل توجه. یک گرافیک فانتزی دیگر را در زیر بررسی کنید و سپس شروع کنیم!

خوشه ‌بندی DBSCAN صورت لبخند

1. DBSCAN با یک نقطه داده شروع دلخواه شروع می شود که بازدید نشده است. همسایگی این نقطه با استفاده از اپسیلون فاصله ε (همه نقاطی که در فاصله ε هستند نقاط همسایگی هستند) استخراج می شود.
2. اگر تعداد کافی نقطه (با توجه به minPoints) در این همسایگی وجود داشته باشد، فرآیند خوشه بندی شروع می شود و نقطه داده فعلی به اولین نقطه در خوشه جدید تبدیل می شود. در غیر این صورت، نقطه به عنوان نویز برچسب گذاری می شود (بعدا این نقطه نویز ممکن است بخشی از خوشه شود). در هر دو مورد آن نقطه به عنوان “بازدید شده” مشخص می شود.
3. برای اولین نقطه در خوشه جدید، نقاط داخل همسایگی فاصله ε آن نیز بخشی از همان خوشه می شوند. این روش برای تعلق همه نقاط در همسایگی ε به یک خوشه، سپس برای تمام نقاط جدیدی که به تازگی به گروه خوشه اضافه شده اند، تکرار می شود.
4. این روند مراحل 2 و 3 تکرار می شود تا زمانی که تمام نقاط خوشه مشخص شوند، یعنی تمام نقاط داخل همسایگی ε خوشه بازدید و برچسب گذاری شده باشند.
5. هنگامی که کار با خوشه فعلی تمام شد، یک نقطه بازدید نشده جدید بازیابی و پردازش می شود که منجر به کشف یک خوشه یا نویز بیشتر می شود. این روند تا زمانی تکرار می شود که همه نقاط به عنوان بازدید شده علامت گذاری شوند. از آنجایی که در پایان این همه نقاط بازدید شده است، هر نقطه به عنوان متعلق به یک خوشه یا نویز مشخص می شود.

DBSCAN مزایای زیادی نسبت به سایر الگوریتم های خوشه بندی دارد. اولا، به هیچ وجه به تعداد خوشه‌ های مجموعه-pe نیاز ندارد. همچنین نقاط پرت را به عنوان نویز شناسایی می کند، بر خلاف میانگین-انتقال که به سادگی آنها را در یک خوشه پرتاب می کند حتی اگر نقطه داده بسیار متفاوت باشد. علاوه بر این، می تواند خوشه هایی با اندازه دلخواه و دلخواه را به خوبی پیدا کند.

اشکال اصلی DBSCAN این است که وقتی خوشه ها دارای چگالی متفاوت هستند، به خوبی سایرین عمل نمی کند. این به این دلیل است که تنظیم آستانه فاصله ε و minPoints برای شناسایی نقاط همسایگی از خوشه ای به خوشه دیگر زمانی که چگالی تغییر می کند متفاوت است. این اشکال همچنین با داده های ابعادی بسیار بالا رخ می دهد زیرا دوباره آستانه فاصله ε برای تخمین چالش برانگیز می شود.

خوشه‌بندی انتظار-بیشینه ‌سازی (EM) با استفاده از مدل ‌های مخلوط گاوسی (GMM)

یکی از ایرادات اصلی k-میانگین استفاده ساده آن از مقدار میانگین برای مرکز خوشه است. با نگاه کردن به تصویر زیر می توانیم بفهمیم که چرا این بهترین راه برای انجام کار ها نیست. در سمت چپ، برای چشم انسان کاملا واضح به نظر می رسد که دو خوشه دایره ای شکل با شعاع های مختلف در مرکز یکسان وجود دارد. k-میانگین نمی تواند این کار را انجام دهد زیرا مقادیر میانگین خوشه ها بسیار نزدیک به هم هستند. k-میانگین همچنین در مواردی که خوشه ها دایره ای نیستند، باز هم در نتیجه استفاده از میانگین به عنوان مرکز خوشه شکست می خورد.

دو مورد شکست برای k-میانگین

مدل ‌های مخلوط گاوسی (GMM) به ما انعطاف ‌پذیری بیشتری نسبت به k-میانگین می‌ دهند. با GMM ها فرض می کنیم که نقاط داده به صورت گاوسی توزیع شده اند. این یک فرض محدود تر از گفتن دایره ای بودن آنها با استفاده از میانگین است. به این ترتیب، ما دو پارامتر برای توصیف شکل خوشه ها داریم: میانگین و انحراف معیار! با در نظر گرفتن یک مثال در دو بعد، به این معنی است که خوشه ها می توانند هر نوع شکل بیضی را به خود بگیرند (زیرا ما یک انحراف معیار در هر دو جهت x و y داریم). بنابراین، هر توزیع گاوسی به یک خوشه اختصاص داده می شود.

برای یافتن پارامتر های گاوسی برای هر خوشه (به عنوان مثال میانگین و انحراف استاندارد)، از یک الگوریتم بهینه‌ سازی به نام انتظار-بیشینه ‌سازی (EM) استفاده خواهیم کرد. به تصویر زیر به عنوان تصویری از برازش گاوسی ها به خوشه ها نگاه کنید. سپس می‌توانیم با استفاده از GMM به فرآیند خوشه‌ بندی انتظار-بیشینه‌ سازی ادامه دهیم.

خوشه ‌بندی EM با استفاده از GMM

1. ما با انتخاب تعداد خوشه ها (مانند k-میانگین) شروع می کنیم و به طور تصادفی پارامتر های توزیع گاوسی را برای هر خوشه مقدار دهی اولیه می کنیم. می توان با نگاهی گذرا به داده ها نیز سعی کرد حدس خوبی برای پارامترهای اولیه ارائه دهد. اگرچه توجه داشته باشید، همانطور که در نمودار بالا مشاهده می شود، این 100٪ ضروری نیست زیرا گاوسی ها ما را بسیار ضعیف شروع می کنند اما به سرعت بهینه می شوند.
2. با توجه به این توزیع های گاوسی برای هر خوشه، احتمال تعلق هر نقطه داده به یک خوشه خاص را محاسبه کنید. هر چه یک نقطه به مرکز گاوس نزدیک ‌تر باشد، احتمال تعلق آن به آن خوشه بیشتر می‌ شود. این باید حس شهودی داشته باشد زیرا با توزیع گاوسی فرض می ‌کنیم که بیشتر داده‌ ها نزدیک ‌تر به مرکز خوشه هستند.
3. بر اساس این احتمالات، مجموعه جدیدی از پارامتر ها را برای توزیع‌ های گاوسی محاسبه می ‌کنیم به طوری که احتمال نقاط داده را در خوشه‌ ها به حداکثر می ‌رسانیم. ما این پارامتر های جدید را با استفاده از مجموع وزنی موقعیت ‌های نقطه داده محاسبه می ‌کنیم، جایی که وزن ‌ها احتمالات نقطه داده متعلق به آن خوشه خاص است. برای توضیح بصری این موضوع می ‌توانیم به گرافیک بالا، به‌ویژه خوشه زرد به عنوان مثال نگاهی بیندازیم. توزیع به طور تصادفی در اولین تکرار شروع می شود، اما می بینیم که بیشتر نقاط زرد در سمت راست آن توزیع قرار دارند. وقتی مجموع وزن شده با احتمالات را محاسبه می کنیم، حتی اگر چند نقطه در نزدیکی مرکز وجود دارد، اکثر آنها در سمت راست قرار دارند. بنابراین به طور طبیعی میانگین توزیع به آن مجموعه نقاط نزدیک‌ تر می‌ شود. همچنین می توانیم ببینیم که بیشتر نقاط “بالا سمت راست به پایین چپ” هستند. بنابراین، انحراف معیار تغییر می‌کند تا بیضی ‌ای را ایجاد کند که با این نقاط برازش بیشتری داشته باشد، تا مجموع وزن ‌شده با احتمالات را به حداکثر برساند.
4. مراحل 2 و 3 به صورت تکراری تا زمان همگرایی تکرار می شوند، جایی که توزیع ها از تکرار به تکرار تغییر زیادی نمی کنند.

2 مزیت کلیدی برای استفاده از GMM وجود دارد. اولا GMM ها از نظر کوواریانس خوشه ای نسبت به k-میانگین بسیار انعطاف پذیرتر هستند. با توجه به پارامتر انحراف استاندارد، خوشه ها می توانند هر شکل بیضی به خود بگیرند، نه اینکه به دایره ها محدود شوند. k-میانگین در واقع یک مورد خاص از GMM است که در آن کوواریانس هر خوشه در تمام ابعاد به 0 نزدیک می شود. بنابراین اگر یک نقطه داده در وسط دو خوشه هم پوشانی قرار دارد، می‌توانیم به سادگی کلاس آن را با گفتن اینکه X درصد به کلاس 1 و Y درصد به کلاس 2 تعلق دارد، تعریف کنیم. یعنی  GMMها از عضویت مختلط پشتیبانی می ‌کنند.

خوشه بندی سلسله مراتبی تجمعی

الگوریتم های خوشه بندی سلسله مراتبی به 2 دسته تقسیم می شوند: از بالا به پایین یا پایین به بالا. الگوریتم های پایین به بالا در ابتدا هر نقطه داده را به عنوان یک خوشه واحد در نظر می گیرند و سپس به طور متوالی جفت های خوشه را ادغام می کنند (یا تجمع می کنند) تا زمانی که همه خوشه ها در یک خوشه واحد که شامل تمام نقاط داده است ادغام شوند. بنابراین، خوشه ‌بندی سلسله مراتبی از پایین به بالا، خوشه ‌بندی تجمعی سلسله مراتبی یا HAC نامیده می‌ شود. این سلسله مراتب خوشه ها به صورت درخت (یا دندروگرام dendrogram) نشان داده می شود. ریشه درخت خوشه منحصر به ‌فردی است که تمام نمونه ‌ها را جمع ‌آوری می‌ کند، برگ ‌ها خوشه ‌هایی هستند که تنها یک نمونه دارند. قبل از رفتن به مراحل الگوریتم، گرافیک زیر را برای یک تصور بررسی کنید.

خوشه بندی سلسله مراتبی تجمعی

1. ما با در نظر گرفتن هر نقطه داده به عنوان یک خوشه شروع می کنیم، یعنی اگر X نقطه داده در مجموعه داده ما وجود داشته باشد، ما خوشه های X داریم. سپس یک متریک فاصله را انتخاب می کنیم که فاصله بین دو خوشه را اندازه می گیرد. به عنوان مثال، از پیوند متوسط ​​استفاده خواهیم کرد که فاصله بین دو خوشه را به عنوان میانگین فاصله بین نقاط داده در خوشه اول و نقاط داده در خوشه دوم تعریف می کند.
2. در هر تکرار، دو خوشه را در یک خوشه ترکیب می کنیم. دو خوشه ای که باید با هم ترکیب شوند به عنوان خوشه هایی با کمترین میانگین پیوند انتخاب می شوند. یعنی با توجه به متریک فاصله انتخابی ما، این دو خوشه کمترین فاصله را بین یکدیگر دارند و بنابراین شبیه ترین هستند و باید با هم ترکیب شوند.
3. مرحله 2 تکرار می شود تا زمانی که به ریشه درخت برسیم، یعنی فقط یک خوشه داریم که شامل تمام نقاط داده است. به این ترتیب ما می‌توانیم تعداد خوشه‌ هایی را که در پایان می ‌خواهیم انتخاب کنیم، فقط با انتخاب زمان توقف ترکیب خوشه ‌ها، یعنی زمانی که ساختن درخت را متوقف می‌ کنیم انتخاب می کنیم!

خوشه‌بندی سلسله مراتبی ما را ملزم نمی‌کند که تعداد خوشه‌ ها را مشخص کنیم و حتی می‌ توانیم انتخاب کنیم که از زمانی که در حال ساختن یک درخت هستیم، کدام تعدادی از خوشه‌ ها بهتر به نظر می ‌رسند. علاوه بر این، الگوریتم به انتخاب متریک فاصله حساس نیست. همه آنها به یک اندازه خوب کار می کنند در حالی که با دیگر الگوریتم های خوشه بندی، انتخاب متریک فاصله بسیار مهم است. یک مورد خوب استفاده از روش های خوشه بندی سلسله مراتبی زمانی است که داده های زیربنایی دارای ساختار سلسله مراتبی هستند و شما می خواهید سلسله مراتب را بازیابی کنید. دیگر الگوریتم های خوشه بندی نمی توانند این کار را انجام دهند. این مزیت‌ های خوشه ‌بندی سلسله مراتبی به قیمت بازده کمتر است، زیرا بر خلاف پیچیدگی خطی k-میانگین و GMM، پیچیدگی زمانی O(n³) دارد.

نتیجه گیری

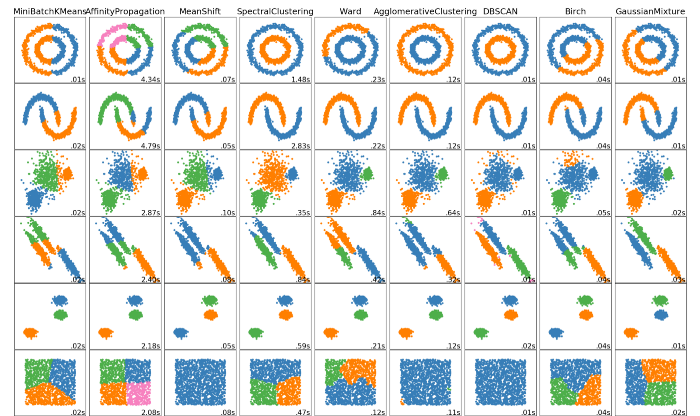
5 الگوریتم خوشه بندی برتر وجود دارد که یک دانشمند داده باید بداند! ما با تجسم عالی از عملکرد این الگوریتم‌ ها و چند الگوریتم دیگر، به لطف Scikit Learn، کار را به پایان خواهیم رساند! جالب است که ببینید الگوریتم های مختلف چگونه با داده های مختلف مقایسه و تضاد دارند!