یادگیری بدون نظارت 1

مقدمه

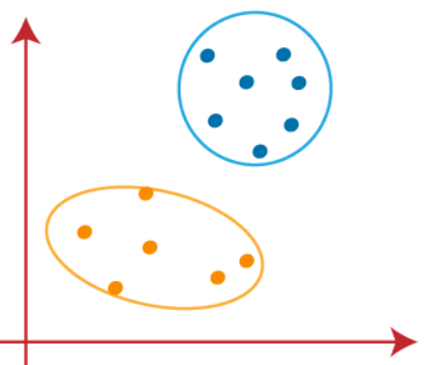
تجزیه و تحلیل خوشه ای یا خوشه بندی یک الگوریتم یادگیری ماشینی بدون نظارت است که مجموعه داده های بدون برچسب را گروه بندی می کند. هدف آن تشکیل خوشه ها یا گروه ها با استفاده از نقاط داده در یک مجموعه داده است به گونه ای که شباهت درون خوشه ای زیاد و شباهت بین خوشه ای کم وجود داشته باشد. در اصطلاح عامیانه، هدف از خوشه ‌بندی تشکیل زیر مجموعه‌ ها یا گروه‌ هایی در یک مجموعه داده متشکل از نقاط داده ‌ای است که واقعا شبیه یکدیگر هستند و گروه ‌ها یا زیر مجموعه‌ ها یا خوشه ‌های تشکیل ‌شده را می ‌توان به طور قابل توجهی از یکدیگر متمایز کرد.

چرا خوشه بندی؟

بیایید فرض کنیم یک مجموعه داده داریم و چیزی در مورد آن نمی دانیم. بنابراین، یک الگوریتم خوشه‌ بندی می‌ تواند گروه‌ هایی از اشیاء را کشف کند که در آن ‌ها میانگین فاصله بین اعضا / نقاط داده هر خوشه نزدیک‌ تر از اعضا / نقاط داده در خوشه ‌های دیگر است.

برخی از کاربرد های عملی خوشه بندی در زندگی واقعی مانند:

1) تقسیم بندی مشتریان: یافتن گروهی از مشتریان با رفتار مشابه با توجه به پایگاه داده بزرگی از مشتریان (یک مثال عملی با استفاده از تقسیم بندی مشتریان بانکی ارائه شده است).

2) طبقه بندی ترافیک شبکه: گروه بندی ویژگی های منابع ترافیک. انواع ترافیک را می توان به راحتی با استفاده از خوشه ها طبقه بندی کرد.

3) فیلتر هرزنامه ایمیل: داده ها با نگاهی به بخش های مختلف (سرصفحه، فرستنده و محتوا) گروه بندی می شوند و سپس می توانند به طبقه بندی اینکه کدام یک از آنها هرزنامه هستند کمک کند.

4) برنامه ریزی شهری: گروه بندی خانه ها بر اساس موقعیت جغرافیایی، ارزش و نوع خانه.

انواع مختلف الگوریتم های خوشه بندی

1) خوشه ‌بندی k-میانگین – با استفاده از این الگوریتم، مجموعه داده های داده شده را از طریق تعداد معینی از خوشه های از پیش تعیین شده یا خوشه های “k” طبقه بندی می کنیم.

2) خوشه بندی سلسله مراتبی – از دو رویکرد تقسیمی و تجمعی پیروی می کند.

تراکم (Agglomerative) هر مشاهده را به عنوان یک خوشه واحد در نظر می گیرد و سپس نقاط داده مشابه را تا زمانی که در یک خوشه ادغام شوند گروه بندی می کند و تقسیمی (Divisive) درست در مقابل آن کار می کند.

3) فازی C به معنای خوشه بندی – عملکرد الگوریتم FCM تقریبا شبیه به الگوریتم خوشه ‌بندی k-میانگین است، تفاوت عمده این است که در FCM یک نقطه داده را می توان در بیش از یک خوشه قرار داد.

4) خوشه بندی فضایی مبتنی بر چگالی – در مناطق کاربردی که به ساختار های خوشه ای غیر خطی نیاز داریم، صرفا بر اساس چگالی مفید است.

اکنون در اینجای این مقاله، ما عمیقا بر روی الگوریتم خوشه ‌بندی k-میانگین، توضیحات نظری عملکرد k-میانگین، مزایا و معایب، و یک مشکل خوشه‌ بندی عملی حل شده تمرکز خواهیم کرد که درک نظری را بهبود می‌ بخشد و دید مناسبی از نحوه کار خوشه ‌بندی k-میانگین به شما ارائه می ‌دهد.

خوشه ‌بندی k-میانگین چیست؟

خوشه ‌بندی k-میانگین یک الگوریتم یادگیری بدون نظارت است که برای گروه بندی مجموعه داده بدون برچسب در خوشه ها / زیر مجموعه های مختلف استفاده می شود.

 

حالا حتما از خود می پرسید که «k» و «means» در خوشه ‌بندی k-میانگین(k-means clustering) چیست؟

 

با استراحت دادن به همه حدس‌ های خود در اینجا، ‘k’ تعداد خوشه‌ های از پیش تعریف ‌شده ‌ای را که باید در فرآیند خوشه‌ بندی ایجاد شوند، مشخص می‌ کند، مثلا اگر k=2 باشد، دو خوشه وجود خواهد داشت و برای k=3، سه خوشه وجود خواهد داشت. خوشه ها و غیره از آنجایی که این یک الگوریتم مبتنی بر مرکز است، «میانگین» در خوشه ‌بندی k-میانگین مربوط به مرکز نقاط داده است که در آن هر خوشه با یک مرکز مرتبط است. مفهوم الگوریتم مبتنی بر مرکز در توضیح عملکرد k-میانگین توضیح داده خواهد شد.

 

به طور عمده الگوریتم خوشه ‌بندی k-میانگین دو کار را انجام می دهد:

• بهینه ترین مقدار را برای نقاط مرکزی K یا مرکز با یک فرآیند تکراری تعیین می کند.
• هر نقطه داده را به نزدیکترین مرکز k خود اختصاص می دهد. خوشه با نقاط داده ای که نزدیک به مرکز k خاص هستند، ایجاد می شود.

خوشه ‌بندی k-میانگین چگونه کار می کند؟

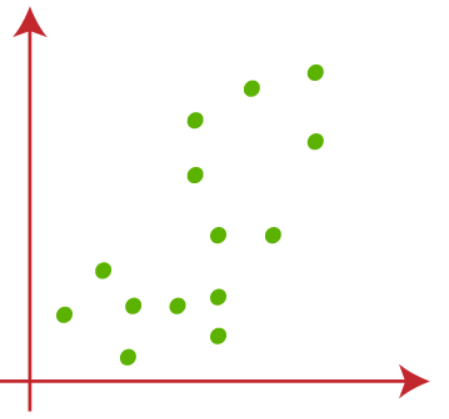
فرض کنید، دو متغیر X1 و X2 داریم، نمودار پراکندگی در زیر آمده است:

(1) اجازه دهید مقدار k که تعداد خوشه های از پیش تعریف شده است را 2 (k=2) در نظر بگیریم، بنابراین در اینجا داده های خود را به 2 خوشه گروه بندی می کنیم.

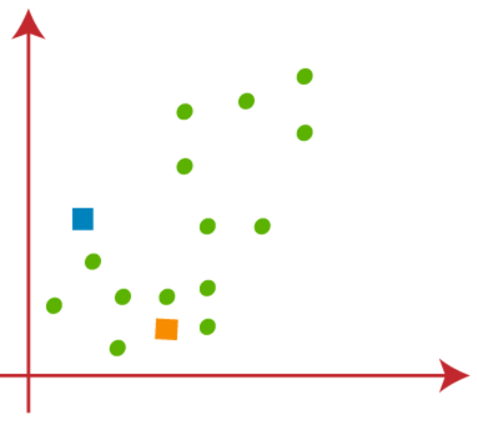
برای تشکیل خوشه ها باید k نقطه به صورت تصادفی انتخاب شود. هیچ محدودیتی در انتخاب نقاط k تصادفی نمی تواند از داخل داده و همچنین خارج باشد. بنابراین، در اینجا ما 2 نقطه را به عنوان نقطه K در نظر می گیریم (که بخشی از مجموعه داده ما نیستند) در شکل زیر نشان داده شده است:

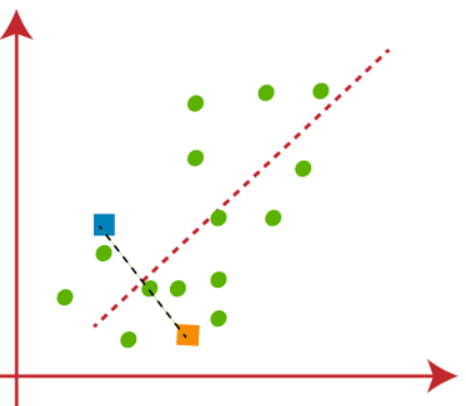
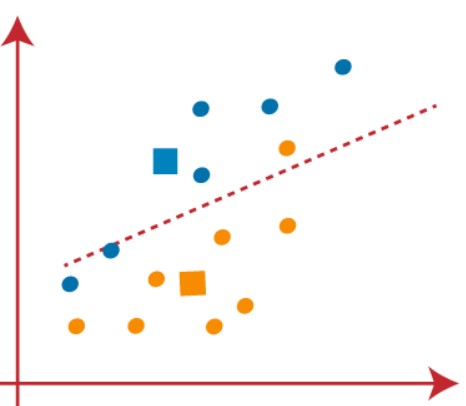
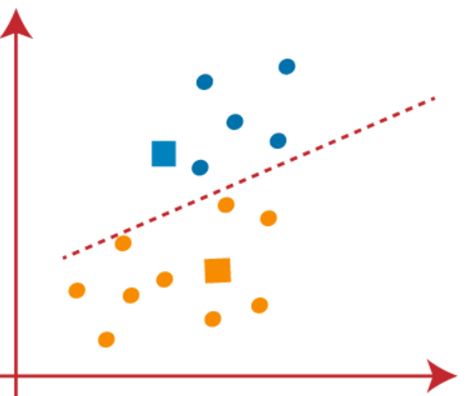
(2) مرحله بعدی اختصاص دادن هر نقطه داده از مجموعه داده در نمودار پراکنده به نزدیکترین نقطه k آن است، این کار با محاسبه فاصله اقلیدسی بین هر نقطه با نقطه k و رسم یک میانه بین هر دو مرکز انجام می شود، که در شکل زیر نشان داده شده است:

ما به وضوح می توانیم مشاهده کنیم که نقطه سمت چپ خط قرمز نزدیک به K1 یا مرکز آبی و نقاط سمت راست خط قرمز نزدیک به K2 یا مرکز نارنجی هستند.

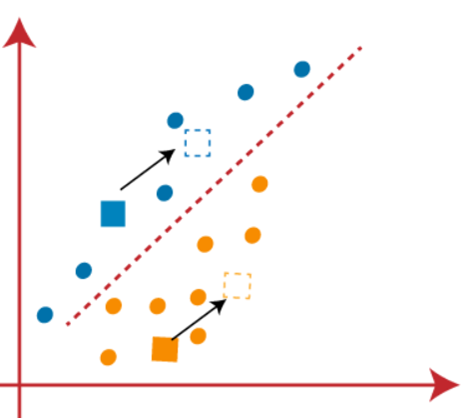
(3) همان طور که باید نزدیکترین نقطه را پیدا کنیم، با انتخاب یک مرکز جدید، این فرآیند را تکرار خواهیم کرد. برای انتخاب مرکز های جدید، مرکز ثقل این مرکز ها را محاسبه کرده و مرکز های جدید را مانند زیر پیدا خواهیم کرد.

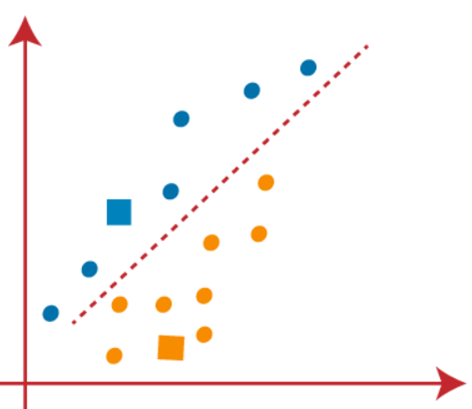
(4) اکنون، باید هر نقطه داده را به یک مرکز جدید اختصاص دهیم. برای این کار، باید همان فرآیند یافتن خط میانه را تکرار کنیم. میانه مانند زیر خواهد بود:

در تصویر بالا می بینیم که یک نقطه نارنجی در سمت چپ خط و دو نقطه آبی رنگ درست در امتداد خط قرار دارند. بنابراین، این سه نقطه به مرکز های جدید اختصاص داده می شود.

ما به یافتن مرکز های جدید ادامه خواهیم داد تا زمانی که هیچ نقطه متفاوتی در دو طرف خط وجود نداشته باشد.

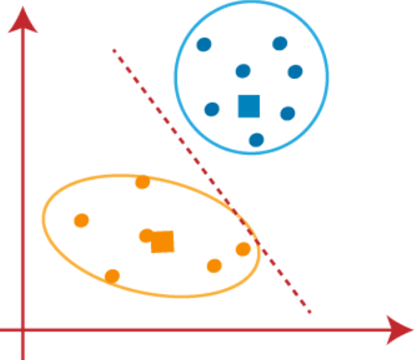
اکنون می توانیم مرکز های فرضی را حذف کنیم. دو خوشه نهایی مانند تصویر زیر خواهند بود:

بنابراین، تا کنون نحوه عملکرد الگوریتم خوشه ‌بندی k-میانگین و مراحل مختلف مربوط به رسیدن به مقصد نهایی خوشه‌ های متمایز را دیده ‌ایم.

 

اکنون همه شما باید تعجب کنید که چگونه مقدار k تعداد خوشه ها را انتخاب کنید؟

عملکرد الگوریتم خوشه ‌بندی k-میانگین به شدت به خوشه هایی که تشکیل می دهد بستگی دارد. انتخاب تعداد بهینه خوشه ها کار دشواری است. راه‌ های مختلفی برای یافتن تعداد بهینه خوشه‌ ها وجود دارد، اما در اینجا ما دو روش برای یافتن تعداد خوشه‌ ها یا مقدار K را مورد بحث قرار می‌ دهیم که عبارت است از روش Elbow و امتیاز Silhouette.

روش Elbow برای یافتن تعداد «k» خوشه‌ ها:[1]

روش Elbow محبوب ترین روش در یافتن تعداد بهینه خوشه ها است، این روش از WCSS (در مجموع مربع ها در خوشه ها) استفاده می کند که کل تغییرات درون یک خوشه را محاسبه می کند.

WCSS= ∑_{Pi in Cluster1} distance (P_i C₁)² +∑_{Pi in Cluster2}distance (P_i C₂)²+∑_{Pi in CLuster3} distance (P_i C₃)²

در فرمول بالا ∑_Pi  در فاصله _Cluster1 (P_i C₁)² مجموع مجذور فواصل بین هر نقطه داده است و مرکز آن در یک cluster₁ است و به طور مشابه برای دو عبارت دیگر در فرمول بالا نیز صدق می کند.

 

مراحل مربوط به روش Elbow:

• خوشه ‌بندی k-میانگین برای مقادیر مختلف k (از 1 تا 10) انجام می شود.
• WCSS برای هر خوشه محاسبه می شود.
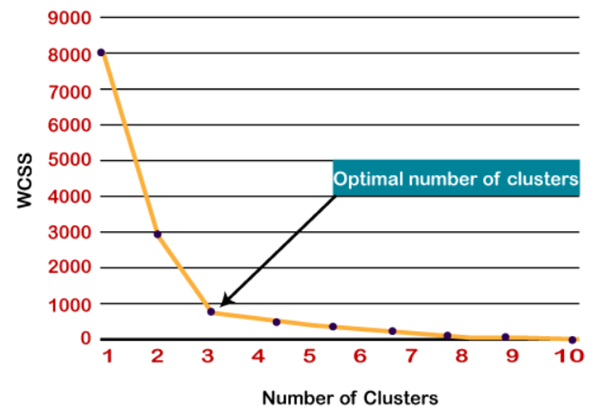
• منحنی بین مقادیر WCSS و تعداد خوشه‌ های k رسم می ‌شود.
• نقطه خم تند یا یک نقطه از طرح شبیه یک بازو است، سپس آن نقطه به عنوان بهترین مقدار K در نظر گرفته می شود.

بنابراین در اینجا همان طور که می بینیم یک خم تند در k=3 است، بنابراین تعداد بهینه خوشه ها 3 می باشد.

 

روش نمره‌ گذاری Silhouette برای یافتن تعداد ‘k‘ خوشه ‌ها

مقدار silhouette معیاری است که نشان می دهد یک هدف چقدر به خوشه خود (انسجام) در مقایسه با خوشه های دیگر (جداسازی) شبیه است. Silhouette از 1- تا 1+ است، جایی که یک مقدار بالا نشان می دهد که هدف به خوبی با خوشه خودش مطابقت دارد و با خوشه های همسایه همخوانی ضعیفی دارد. اگر بیشتر هدف ها دارای ارزش بالایی هستند، پیکر بندی خوشه بندی مناسب است. اگر بسیاری از نقاط دارای مقدار کم یا منفی باشند، ممکن است پیکر بندی خوشه ‌بندی، خوشه ‌های خیلی زیاد یا خیلی کم داشته باشد.

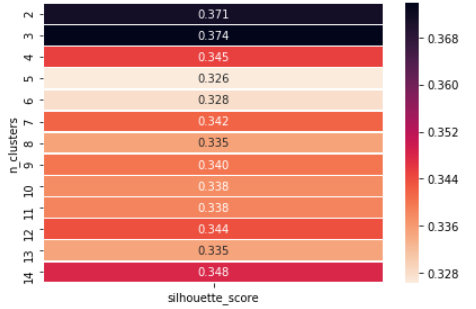
مثالی که نشان می‌ دهد چگونه می ‌توانیم مقدار “k” را انتخاب کنیم، زیرا می ‌بینیم که در n=3 حداکثر امتیاز Silhouette را داریم، بنابراین مقدار k = 3 را انتخاب می‌کنیم.

 

مزایای استفاده از خوشه ‌بندی k-میانگین

• پیاده سازی آسان
• با تعداد زیادی متغیر، k-میانگین ممکن است از نظر محاسباتی سریعتر از خوشه بندی سلسله مراتبی باشد (اگر K کوچک باشد).
• k-میانگین ممکن است خوشه های بالاتری نسبت به خوشه بندی سلسله مراتبی ایجاد کند.

 

معایب استفاده از خوشه ‌بندی k-میانگین

• پیش بینی تعداد خوشه ها مشکل است (مقدار k).
• دانه های اولیه تاثیر زیادی بر نتایج نهایی دارند.

 

پیاده سازی عملی الگوریتم خوشه ‌بندی k-میانگین با استفاده از پایتون (بخش بندی مشتریان بانکی)

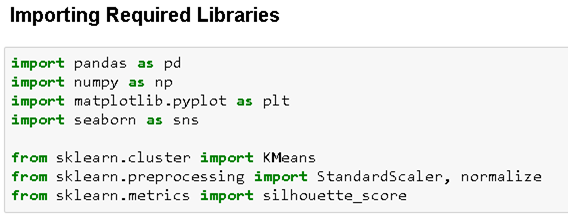
در اینجا ما کتابخانه های مورد نیاز را برای تجزیه و تحلیل های خود وارد می کنیم.

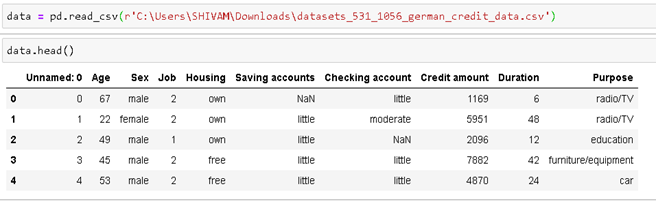
خواندن داده ها و دریافت 5 مشاهدات برتر برای نگاهی به مجموعه داده ها.

کد EDA (تجزیه و تحلیل داده های اکتشافی) گنجانده نشده است، EDA بر روی این داده ها انجام شد و تجزیه و تحلیل پرت برای پاک کردن داده ها و متناسب کردن آن برای تجزیه و تحلیل ما انجام شد.

همان طور که می دانیم که میانگین K فقط بر روی داده های عددی انجام می شود، بنابراین ما ستون های عددی را برای تجزیه و تحلیل خود انتخاب می کنیم.

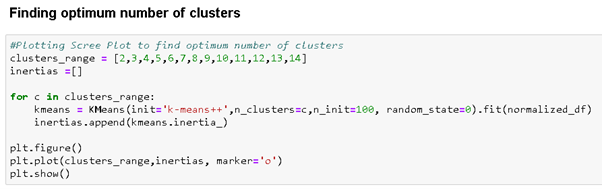
اکنون برای اجرای خوشه ‌بندی k-میانگین همان طور که قبلا در این مقاله بحث شد، باید مقدار ‘k’ تعداد خوشه ها را پیدا کنیم و می توانیم این کار را با استفاده از کد زیر انجام دهیم، در اینجا از چندین مقدار k برای خوشه بندی استفاده می کنیم و سپس با استفاده از روش Elbow، آن را انتخاب می کنیم.

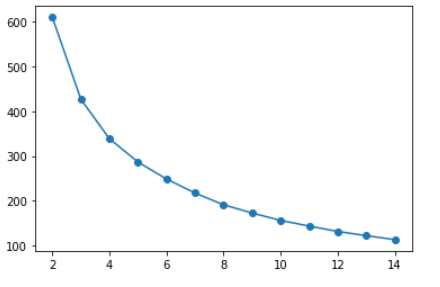
با افزایش تعداد خوشه ها، واریانس (در مجموع مربعات خوشه ای) کاهش می یابد. Elbow در 3 یا 4 خوشه نشان دهنده مقرون به صرفه ترین تعادل بین به حداقل رساندن تعداد خوشه ها و به حداقل رساندن واریانس در هر خوشه است، بنابراین می توانیم مقدار k را 3 یا 4 انتخاب کنیم.

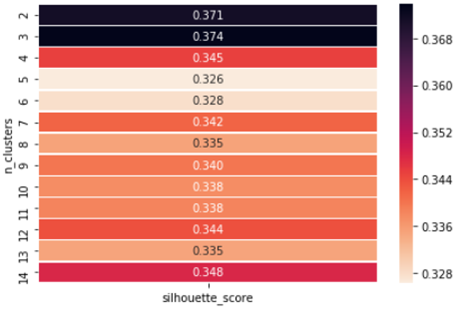
اکنون نشان می دهیم که چگونه می توانیم از روش مقدار Silhouette برای یافتن مقدار ‘k’ استفاده کنیم.

 

اگر مشاهده کنیم، تعداد بهینه خوشه ها را در n = 3 به دست می آوریم تا در نهایت بتوانیم مقدار k = 3 را انتخاب کنیم.

 

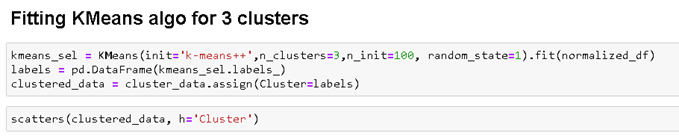
اکنون، برازش الگوریتم k با استفاده از مقدار k=3 و ترسیم نقشه گرمایی یا رنگی(heatmap) برای خوشه‌ ها را انجام می دهیم.

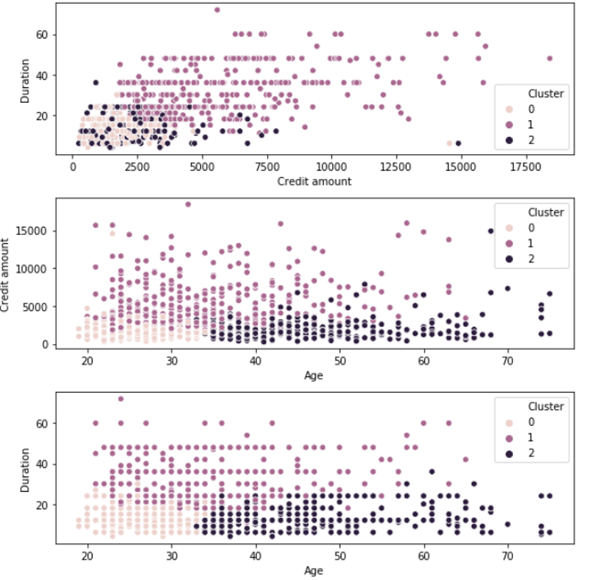
تحلیل نهایی

خوشه 0 – مشتریان جوانی که وام های اعتباری کم را برای مدت کوتاهی دریافت می کنند

 

خوشه 1 – مشتریان میانسال که وام های اعتباری بالا برای مدت طولانی دریافت می کنند

 

خوشه 2 – مشتریان مسن که وام های اعتباری متوسط ​​را برای مدت کوتاهی دریافت می کنند.