نرمال سازی 2

به قسمت 1 از آموزش جامع در یادگیری عمیق خوش آمدید. این آموزش یا راهنما بیشتر برای افراد مبتدی است و سعی شده تا حد ممکن بر موضوعات تعریف و تاکید شود. از آنجا که یادگیری عمیق یک موضوع بسیار بزرگ است، کل آموزش به چند بخش تقسیم شده است. حتما در صورت مفید بودن این قسمت، قسمت های دیگر را مطالعه کنید.

محتویات

1. مقدمه

• یادگیری عمیق چیست؟
• چرا یادگیری عمیق؟
• چه مقدار از داده ها بزرگ است؟
• زمینه هایی که در آن یادگیری عمیق استفاده می شود
• تفاوت یادگیری عمیق و یادگیری ماشینی

2. وارد کردن کتاب خانه های لازم
3. بررسی کلی
4. پس نمایی استدلالی (Logistic Regression)

• گراف محاسباتی (Computational graph)
• پارامترهای اولیه سازی (Initializing parameters)
• پیش انتشار (Forward Propagation)
• بهینه سازی با نزول گرادیان (Optimizing with Gradient Descent)

5. پس نمایی استدلالی با استفاده از Sklearn (Logistic Regression with Sklearn)

مقدمه

یادگیری عمیق چیست؟

• یادگیری عمیق زیرشاخه ‌ای از یادگیری ماشینی است که از نورون ‌های بیولوژیکی مغز الهام گرفته شده و آن را به شبکه‌ های عصبی مصنوعی با یادگیری بازنمایی ترجمه می‌کنند.

چرا یادگیری عمیق؟

• وقتی حجم داده‌ ها افزایش می ‌یابد، تکنیک‌ های یادگیری ماشینی، مهم نیست که چقدر بهینه شده ‌اند، شروع به نا کارآمدی از نظر عملکرد و دقت می‌کنند، در حالی که یادگیری عمیق در چنین مواردی بسیار بهتر عمل می‌کند.

چه مقدار از داده، بزرگ است؟

• نمی توان آستانه ای را برای بزرگ نامیدن داده ها تعیین کرد، اما به طور شهودی فرض کنید یک میلیون نمونه ممکن است برای گفتن “بزرگ است” کافی باشد.

زمینه هایی که از DL استفاده می شود

• طبقه بندی تصویر، تشخیص گفتار، NLP (پردازش زبان طبیعی)، سیستم های توصیه و غیره.

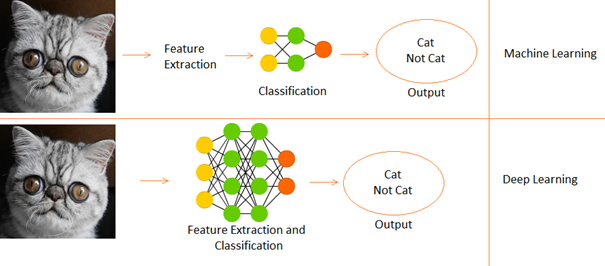
تفاوت بین یادگیری عمیق و یادگیری ماشینی

• یادگیری عمیق زیر مجموعه ای از یادگیری ماشینی است.
• در یادگیری ماشینی ویژگی ها به صورت دستی ارائه می شوند.
• در حالی که یادگیری عمیق ویژگی ها را مستقیما از داده ها یاد می گیرد.

ما از مجموعه داده ارقام زبان اشاره که در Kaggle موجود است استفاده خواهیم کرد. حالا بیایید شروع کنیم.

وارد کردن کتاب خانه های مورد نیاز

import numpy as np # linear algebra

import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)

import matplotlib.pyplot as plt

# Input data files are available in the “../input/” directory.

# import warnings

import warnings

# filter warnings

warnings.filterwarnings(‘ignore’)

from subprocess import check_output

print(check_output([“ls”, “../input”]).decode(“utf8”))

# Any results you write to the current directory are saved as output.

مروری بر داده ها

• 2062 تصویر رقمی زبان اشاره در این مجموعه داده وجود دارد.
• از آنجایی که 10 رقم از 0 تا 9 وجود دارد، 10 تصویر رقمی زبان اشاره منحصر به فرد وجود دارد.
• در ابتدا، ما فقط از 0 و 1 استفاده می کنیم (برای ساده نگه داشتن آموز برای زبان آموزان)
• در داده ها علامت عقربه برای 0 بین شاخص های 204 و 408 قرار دارد. 205 نمونه برای 0 وجود دارد.
• همچنین علامت عقربه برای 1 بین شاخص های 822 و 1027 است. تعداد 206 نمونه می باشد.
• بنابراین ما از 205 نمونه از هر کلاس استفاده خواهیم کرد (توجه: در واقع 205 نمونه برای یک مدل یادگیری عمیق بسیار کمتر است، اما از آن جایی که این یک آموزش است، می توانیم آن را نادیده بگیریم).

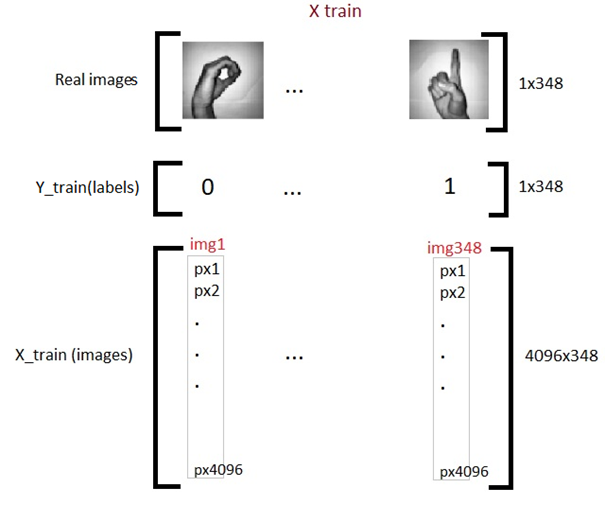
اکنون آرایه‌ های X و Y خود را آماده می کنیم که X آرایه تصویر (ویژگی ها) و Y آرایه برچسب (0 و1) ما می باشد.

1.

# load data set

x_l = np.load(‘../input/Sign-language-digits-dataset/X.npy’)

Y_l = np.load(‘../input/Sign-language-digits-dataset/Y.npy’)

img_size = 64

plt.subplot(1, 2, 1)

plt.imshow(x_l[260].reshape(img_size, img_size))

plt.axis(‘off’)

plt.subplot(1, 2, 2)

plt.imshow(x_l[900].reshape(img_size, img_size))

plt.axis(‘off’)

# Join a sequence of arrays along an row axis.

# from 0 to 204 is zero sign and from 205 to 410 is one sign

X = np.concatenate((x_l[204:409], x_l[822:1027] ), axis=0)

z = np.zeros(205)

o = np.ones(205)

Y = np.concatenate((z, o), axis=0).reshape(X.shape[0],1)

print(“X shape: ” , X.shape)

print(“Y shape: ” , Y.shape)

برای ایجاد آرایه X، ما ابتدا بخش هایی از 0 ها و 1 ها از تصاویر علامت اشاره دست از مجموعه داده را برش داده و به آرایه X الحاق می کنیم. سپس کاری مشابه با آرایه Y انجام می دهیم، اما به جای آن از برچسب‌ ها استفاده می‌کنیم.

1. بنابراین می بینیم که شکل آرایه X (410, 64, 64) می باشد.

• 410 به معنی 205 تصویر از 0 و 205 تصویر از 1 است.
• 64 به معنی این است که اندازه تصویر ما 64 x 64 پیکسل است.

2. شکل Y (410.1) است؛ بنابراین 410 1 ها و 0 ها.
3. حال X وY را به مجموعه های آموزش (یا سلسله) (train) و آزمایش (test) تقسیم می کنیم.

• آموزش = 75%، آموزش = 15%
• random_state =: هنگام تصادفی سازی از یک دانه خاص استفاده می کند، بنابراین اگر سلول چندین بار اجرا شود، عدد تصادفی تولید شده هر بار تغییر نمی کند. هر بار همان آزمون و توضیع سلسله ایجاد می شود.

# Then lets create x_train, y_train, x_test, y_test arrays

from sklearn.model_selection import train_test_split

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.15, random_state=42)

number_of_train = X_train.shape[0]

number_of_test = X_test.shape[0]

ما یک آرایه ورودی سه بعدی داریم، بنابراین باید آن را به دو بعدی مسطح کنیم تا به اولین مدل یادگیری عمیق ما وارد شود. از آن جایی که Y از قبل دو بعدی است، آن را همان طور که هست رها می کنیم.

X_train_flatten = X_train.reshape(number_of_train,X_train.shape[1]*X_train.shape[2])

X_test_flatten = X_test .reshape(number_of_test,X_test.shape[1]*X_test.shape[2])

print(“X train flatten”,X_train_flatten.shape)

print(“X test flatten”,X_test_flatten.shape)

اکنون ما مجموعا 348 تصویر داریم که هر کدام دارای 4096 پیکسل در آرایه آموزشی X داریم. و 62 تصویر با همان تراکم پیکسلی 4096 در آرایه آزمایشی داریم. حالا آرایه ها را جا بجا می کنیم. این فقط یک انتخاب شخصی است و در کد های بعدی خواهید دید که چرا این کار را انجام می دهیم.

x_train = X_train_flatten.T

x_test = X_test_flatten.T

y_train = Y_train.T

y_test = Y_test.T

print(“x train: “,x_train.shape)

print(“x test: “,x_test.shape)

print(“y train: “,y_train.shape)

print(“y test: “,y_test.shape)

بنابراین اکنون کار آماده سازی داده های مورد نیاز خود را به پایان رسانده ایم. بدین گونه:

اکنون با یکی از مدل های اساسی Dl به نام پس نمایی استدلالی یا Logistic Regression آشنا خواهیم شد.

 

پس نمایی استدلالی (Logistic Regression)

هنگام صحبت کردن در مورد طبقه بندی دودویی یا باینری، اولین مدلی که به ذهن می رسد رگرسیون لجستیک است. اما یکی ممکن است متعجب شود که استفاده از رگرسیون لجستیک در یادگیری عمیق است چیست؟ پاسخ ساده است از آن جایی که رگرسیون لجستیک یک شبکه عصبی ساده است؛ اصطلاحات شبکه عصبی و یادگیری عمیق مرتبط هستند و با هم می آیند. برای درک رگرسیون لجستیک، ابتدا باید در مورد گراف های محاسباتی یاد بگیریم.

گراف های محاسباتی

گراف های محاسباتی را می توان به عنوان یک راه تصویری برای نشان دادن عبارات ریاضی در نظر گرفت. این را با یک مثال توضیح می دهیم. فرض کنید یک عبارت ریاضی ساده داریم؛ مانند:

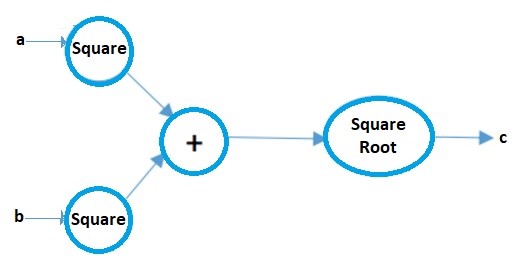
c = ( a² + b² ) ^½

نمودار محاسباتی آن تصویر زیر خواهد بود:

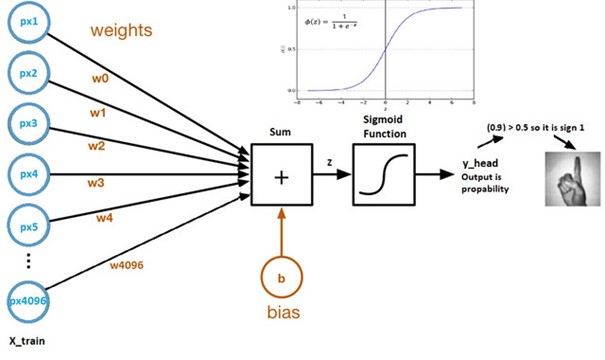
حال نمودار محاسباتی رگرسیون لجستیک را مشاهده می کنیم:

منبع تصویر: مجموعه داده Kaggle

• وزن و سو گیری پارامتر های مدل نامیده می شوند.
• وزن ها ضرایب هر پیکسل را نشان می دهند.
• سو گیری وقفه منحنی است که با ترسیم پارامتر ها در برابر برچسب ها ایجاد می شود.
• Z = (px1*wx1) + (px2*wx2) + …. +(px4096*wx4096)
• y_head = sigmoid_funtion(Z)
• کاری که تابع سیگموئید انجام می دهد اساسا مقدار Z را بین 0 و 1 مقیاس می دهد، بنابراین به یک احتمال تبدیل می شود.

چرا از تابع سیگموئید استفاده کنیم؟

• یک نتیجه احتمالی به ما می دهد.
• از آن جایی که یک مشتق است، می توانیم از آن در الگوریتم نزول گرادیان استفاده کنیم.

حال هر یک از اجزای نمودار محاسباتی فوق را به تفصیل بررسی می کنیم.

مقدار دهی اولیه پارامتر ها

منبع تصویر: Microsoft Docs

هر پیکسل وزن خاص خود را دارد. اما سوال این است که وزن اولیه آنها چه خواهد بود؟ تکنیک های متعددی برای انجام این کار وجود دارد که در قسمت 2 این مقاله پوشش داده شده است اما در حال حاضر ، ما می توانیم آنها را با استفاده از هر مقدار تصادفی اولیه مقدار دهی می کنیم. بر فرض 0.01.

شکل آرایه وزن ها (4096,1) خواهد بود، از آنجا که در مجموع 4096 پیکسل در هر تصویر وجود دارد، و اجازه دهید سوگیری اولیه 0 باشد.

# lets initialize parameters

# So what we need is dimension 4096 that is number of pixels as a parameter for our initialize method(def)

def initialize_weights_and_bias(dimension):

    w = np.full((dimension,1),0.01)

    b = 0.0

    return w, b

w,b = initialize_weights_and_bias(4096)

پیش انتشار (Forward Propagation)

به تمام مراحل از پیکسل ها تا تابع هزینه، پیش انتشار گفته می شود.

برای محاسبه Z از فرمول Z = (w.T)x + b استفاده می کنیم؛  که در آن x آرایه پیکسل، وزن w، و b سوگیری است. پس از محاسبه Z ما آن را به تابع سیگموئید که آن را به y_head (احتمال) باز می گرداند وارد می کنیم. پس از آن تابع loss(error) (اتلاف، ضرر) را محاسبه می کنیم.

تابع هزینه جمع تمام زیان ها است و مدل را برای پیش بینی های اشتباه مجازات می کند. بدین گونه مدل ما پارامتر ها را یاد می گیرد.

# calculation of z

#z = np.dot(w.T,x_train)+b

def sigmoid(z):

    y_head = 1/(1+np.exp(-z))

    return y_head

y_head = sigmoid(0)

y_head

عبارت ریاضی برای تابع از دست دادن(log) عبارت است از:

همان طور که قبلا اشاره شده، آنچه تابع از دست دادن اساسا انجام می دهد مجازات برای پیش بینی های اشتباه است. این کد برای پیش انتشار می باشد:

# Forward propagation steps:

# find z = w.T*x+b

# y_head = sigmoid(z)

# loss(error) = loss(y,y_head)

# cost = sum(loss)

def forward_propagation(w,b,x_train,y_train):

    z = np.dot(w.T,x_train) + b

    y_head = sigmoid(z) # probabilistic 0-1

    loss = -y_train*np.log(y_head)-(1-y_train)*np.log(1-y_head)

    cost = (np.sum(loss))/x_train.shape[1]      # x_train.shape[1]  is for scaling

    return cost

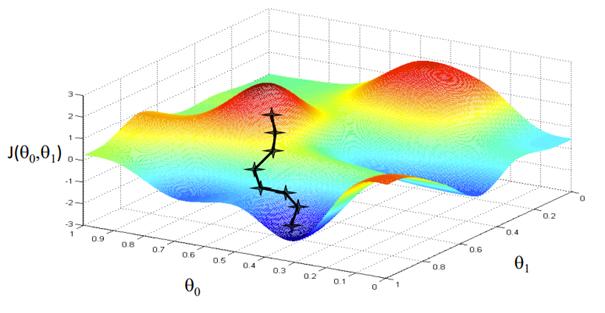
بهینه سازی با نزول گرادیان

منبع تصویر:  Coursera

هدف ما یافتن مقادیری برای پارامتر هایمان است که تابع ضرر در آن  حداقل است. معادله برای نزول گرادیان:

که در آن “w” وزن یا پارامتر رانشان می دهد. حرف یونانی آلفا “stepsize” نامیده می شود. آلفا اندازه تکرار هایی را که هنگام پایین رفتن از شیب برای یافتن حداقل های محلی یا موضعی انجام می دهیم را نشان می دهد. بقیه آن ها مشتق تابع ضرر است که به عنوان گرادیان نیز شناخته می شود. الگوریتم برای نزول گرادیان ساده است:

1. ابتدا یک نقطه داده تصادفی در نمودار خود می گیریم و شیب آن را پیدا می کنیم.
2. سپس جهت کاهش تابع، کاهش ارزش را پیدا می کنیم.
3. وزن ها را با استفاده از فرمول بالا به روز کنید. (به این روش پس انتشار نیز می گویند)
4. نقطه بعدی را با اندازه گام α انتخاب کنید.
5. تکرار کنید.

# In backward propagation we will use y_head that found in forward progation

# Therefore instead of writing backward propagation method, lets combine forward propagation and backward propagation

def forward_backward_propagation(w,b,x_train,y_train):

    # forward propagation

    z = np.dot(w.T,x_train) + b

    y_head = sigmoid(z)

    loss = -y_train*np.log(y_head)-(1-y_train)*np.log(1-y_head)

    cost = (np.sum(loss))/x_train.shape[1]      # x_train.shape[1]  is for scaling

    # backward propagation

    derivative_weight = (np.dot(x_train,((y_head-y_train).T)))/x_train.shape[1] # x_train.shape[1]  is for scaling

    derivative_bias = np.sum(y_head-y_train)/x_train.shape[1]                 # x_train.shape[1]  is for scaling

    gradients = {“derivative_weight”: derivative_weight,”derivative_bias”: derivative_bias}

    return cost,gradients

حالا پارامتر های یادگیری را به روز می کنیم:

# Updating(learning) parameters

def update(w, b, x_train, y_train, learning_rate,number_of_iterarion):

    cost_list = []

    cost_list2 = []

    index = []

    # updating(learning) parameters is number_of_iterarion times

    for i in range(number_of_iterarion):

        # make forward and backward propagation and find cost and gradients

        cost,gradients = forward_backward_propagation(w,b,x_train,y_train)

        cost_list.append(cost)

        # lets update

        w = w – learning_rate * gradients[“derivative_weight”]

        b = b – learning_rate * gradients[“derivative_bias”]

        if i % 10 == 0:

            cost_list2.append(cost)

            index.append(i)

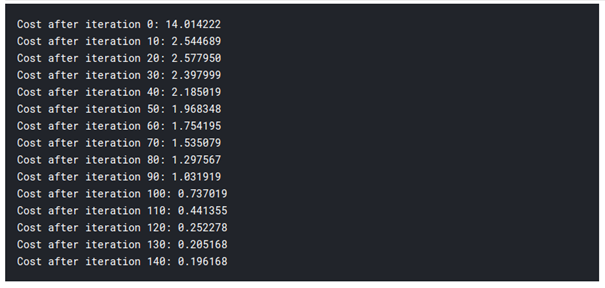
            print (“Cost after iteration %i: %f” %(i, cost))

    # we update(learn) parameters weights and bias

    parameters = {“weight”: w,”bias”: b}

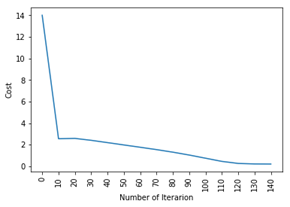
    plt.plot(index,cost_list2)

    plt.xticks(index,rotation=’vertical’)

    plt.xlabel(“Number of Iterarion”)

    plt.ylabel(“Cost”)

    plt.show()

    return parameters, gradients, cost_list

parameters, gradients, cost_list = update(w, b, x_train, y_train, learning_rate = 0.009,number_of_iterarion = 200)

تا این مرحله، ما پارامتر های خود را یاد گرفتیم. يعني ما داريم داده ها را جا ميديم. در مرحله پیش بینی، ما یک x_test ورودی داریم و

با استفاده از آن، ما پیش بینی های پیشین را انجام می دهیم.

# prediction

def predict(w,b,x_test):

    # x_test is a input for forward propagation

    z = sigmoid(np.dot(w.T,x_test)+b)

    Y_prediction = np.zeros((1,x_test.shape[1]))

    # if z is bigger than 0.5, our prediction is sign one (y_head=1),

    # if z is smaller than 0.5, our prediction is sign zero (y_head=0),

    for i in range(z.shape[1]):

        if z[0,i]<= 0.5:

            Y_prediction[0,i] = 0

        else:

            Y_prediction[0,i] = 1

predict(parameters[“weight”],parameters[“bias”],x_test)

 

حال ما پیش بینی هایمان را انجام می دهیم. همه چيز را کنار هم می گذاريم:

def logistic_regression(x_train, y_train, x_test, y_test, learning_rate ,  num_iterations):

    # initialize

    dimension =  x_train.shape[0]  # that is 4096

    w,b = initialize_weights_and_bias(dimension)

    # do not change learning rate

    parameters, gradients, cost_list = update(w, b, x_train, y_train, learning_rate,num_iterations)

    y_prediction_test = predict(parameters[“weight”],parameters[“bias”],x_test)

    y_prediction_train = predict(parameters[“weight”],parameters[“bias”],x_train)

    # Print train/test Errors

    print(“train accuracy: {} %”.format(100 – np.mean(np.abs(y_prediction_train – y_train)) * 100))

    print(“test accuracy: {} %”.format(100 – np.mean(np.abs(y_prediction_test – y_test)) * 100))

   logistic_regression(x_train, y_train, x_test, y_test,learning_rate = 0.01, num_iterations = 150)

 

بنابراین همان طور که می بینید، حتی اساسی ترین مدل یادگیری عمیق کاملا سخت است. یاد گیری این آسان نیست، و افراد مبتدی ممکن است هنگام آموزش این موضوع به صورت فشرده احساس سردرگمی کنند، اما موضوع این است که ما حتی هنوز به یادگیری عمیق نزدیک نشده ایم، این آموزش ها مانند سطح آن است. مطالب بیشتری در این مورد وجود دارد که در قسمت دوم این مقاله آموزش داده خواهد شد.

از آنجا که ما منطق پشت رگرسیون لجستیک را آموخته ایم، می توانیم از کتابخانه ای به نام SKlearn استفاده کنیم که در حال حاضر بسیاری از مدل ها و الگوریتم های ساخته شده را در خود دارد، بنابراین لازم نیست همه چیز را از ابتدا شروع کنید.

رگرسیون لجستیک با استفاده از SKlearn

در این بخش مطلب زیادی توضیح داده زیرا تقریبا تمام منطق و شهود پشت رگرسیون لجستیک را می دانید. اگر علاقه مند به مطالعه در مورد کتابخانه Sklearn هستید، می توانید اسناد رسمی را در اینجا بخوانید.

این کد در زیر آمده است، و من مطمئنا از دیدن اینکه چقدر تلاش کمی نیاز دارد، شگفت زده خواهید شد:

from sklearn import linear_model

logreg = linear_model.LogisticRegression(random_state = 42,max_iter= 150)

print(“test accuracy: {} “.format(logreg.fit(x_train.T, y_train.T).score(x_test.T, y_test.T)))

print(“train accuracy: {} “.format(logreg.fit(x_train.T, y_train.T).score(x_train.T, y_train.T)))

بله! این تمام چیزی است که نیاز دارید، فقط 1 خط کد!