سری های زمانی (TS)

مرور کلی

• مراحل ایجاد پیش ‌بینی سری زمانی را بیاموزید
• تمرکز بیشتر بر روی مدل ‌های تست دیکی فولر (Dickey-Fuller) و ARIMA (خود ارجاع یا اتو رگرسیون، میانگین متحرک).
• مفاهیم را به صورت تئوری و همچنین با اجرای آنها در پایتون یاد بگیرید

 مقدمه

سری زمانی Time Series (که از هم اکنون به عنوان TS نامیده می شود) به عنوان یکی از مهارت های کمتر شناخته شده در حوزه علم داده در نظر گرفته می شود (حتی من چند روز پیش سرنخ کمی در مورد آن داشتم). من خود را برای یادگیری گام‌ های اساسی، برای حل یک مشکل سری زمانی راهی سفر کردم و در اینجا یافته های خود را با شما به اشتراک می ‌گذارم. اینها قطعا به شما کمک می‌ کنند تا در هر پروژه ‌ای که در آینده انجام خواهید داد، مدل مناسبی داشته باشید.

قبل از مرور این مقاله، خواندن یک آموزش کامل در مورد مدل سازی سری های زمانی در R و شرکت در دوره رایگان پیش بینی سری های زمانی را به شدت توصیه می کنم. این مبحث ها بر مفاهیم اساسی تمرکز دارد و من روی استفاده از این مفاهیم در حل یک مشکل از صفر تا صد همراه با کد های پایتون تمرکز خواهم کرد. منابع زیادی برای سری های زمانی در R وجود دارد، اما تعداد بسیار کمی برای پایتون وجود دارد، بنابراین من در این مقاله از پایتون استفاده خواهم کرد.

آیا شما یک مبتدی به دنبال جایی برای شروع سفر علم داده خود هستید؟ در اینجا یک دوره جامع برای کمک به شما در این سفر وجود دارد. سری زمانی استاد، یادگیری ماشینی و یادگیری عمیق از طریق برنامه تایید شده Blackbelt ما

• برنامه تایید شده AI & ML Blackbelt+

فهرست مطالب:

1. چه چیزی سریال های زمانی را خاص می کند؟
2. بارگیری و مدیریت سری های زمانی در پانداها
3. چگونه ثابت بودن یک سری زمانی را بررسی کنیم؟
4. چگونه یک سری زمانی ثابت بسازیم؟
5. پیش بینی یک سری زمانی

 

1. چه چیزی سریال های زمانی را خاص می کند؟

همان طور که از نام آن پیداست، TS مجموعه ای از نقاط داده است که در بازه های زمانی ثابت جمع آوری می شوند. اینها برای تعیین روند بلند مدت تجزیه و تحلیل می شوند تا آینده را پیش بینی کنند یا شکل دیگری از تجزیه و تحلیل را انجام دهند. اما چه چیزی یک TS را با مشکل رگرسیون معمولی متفاوت می کند؟ 2 چیز وجود دارد:

1. وابسته به زمان است. بنابراین فرض اصلی یک مدل رگرسیون خطی مبنی بر اینکه مشاهدات مستقل هستند در این مورد صادق نیست.
2. همراه با روند افزایشی یا کاهشی، اکثر TS ها نوعی روند فصلی دارند، به عبارتی دیگر تغییرات خاص برای یک بازه زمانی خاص؛ به عنوان مثال، اگر فروش یک ژاکت پشمی را در طول زمان مشاهده کنید، همیشه در فصل زمستان فروش بیشتری خواهید داشت.

به دلیل ویژگی های ذاتی یک TS، مراحل مختلفی در تجزیه و تحلیل آن وجود دارد. در ادامه به تفصیل به این موارد پرداخته شده است. بیایید با بارگذاری یک هدف TS در پایتون شروع کنیم. ما از مجموعه داده محبوب AirPassengers استفاده می کنیم که می توانید از اینجا دانلود کنید.

لطفا توجه داشته باشید که هدف این مقاله آشنایی شما با تکنیک های مختلف مورد استفاده برای TS به طور کلی است. مثالی که در اینجا در نظر گرفته شده است فقط برای توضیح است و من بر پوشش گسترده موضوعات تمرکز خواهم کرد و پیش بینی خیلی دقیقی ندارم.

 

2. بارگیری و مدیریت سری های زمانی در پاندا ها

Pandas کتابخانه‌ های اختصاصی برای مدیریت اهداف TS دارد، به‌ویژه کلاس datatime64[ns] که اطلاعات زمان را ذخیره می‌ کند و به ما اجازه می ‌دهد تا برخی از عملیات ‌ها را واقعا سریع انجام دهیم. بیایید با فعال کردن کتابخانه های مورد نیاز شروع کنیم.

1#  importing required libraries

2 import pandas as pd

3 import numpy as np

4

5 # Now, we will load the data set and look at some initial rows and data types of the columns:

6 data = pd.read_csv(‘AirPassengers.csv’)

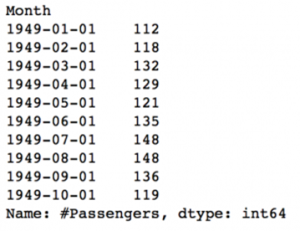
7 print (data.head())

8 print (‘\n Data Types:’)

9 print (data.dtypes)

10

11  #The data contains a particular month and number of passengers travelling in that month. In order to read the data as a time series, we have to pass special arguments to the read_csv command:

12 dateparse = lambda dates: pd.datetime.strptime(dates, ‘%Y-%m’)

13 data = pd.read_csv(‘AirPassengers.csv’, parse_dates=[‘Month’], index_col=’Month’,date_parser=dateparse)

14 print (‘\n Parsed Data:’)

15 print (data.head())

16

17 ## NOTE: You can run remaining codes in this article as well, using this live coding window.

بیایید استدلال ها را یکی یکی درک کنیم:

1. parse_dates: ستونی را مشخص می کند که حاوی اطلاعات تاریخ است. همانطور که در بالا گفتیم، نام ستون “ماه” است.
2. index_col: یک ایده کلیدی در مورد استفاده از پاندا ها برای داده های TS این است که شاخص باید متغیری باشد که اطلاعات تاریخ زمان را نشان می دهد. بنابراین این استدلال به پاندا ها می گوید که از ستون “ماه” به عنوان شاخص استفاده کنند.
3. date_parser: تابعی را مشخص می کند که یک رشته ورودی را به متغیر datetime تبدیل می کند. باید بدانید که پاندا ها داده ‌ها را در قالب «YYYY MM DD HH:MM:SS» می‌خواند. اگر داده ها در این فرمت نیستند، فرمت باید به صورت دستی تعریف شود. برای این منظور می توان از چیزی شبیه به تابع dataparse تعریف شده در اینجا استفاده کرد.

اکنون می بینیم که داده ها دارای هدف زمان به عنوان شاخص و Passengers# به ​​عنوان ستون هستند. با دستور زیر می توانیم نوع داده شاخص را بررسی کنیم:

به dtype=’datetime[ns]’ توجه کنید که تأیید می کند که یک هدف  datetime است. به عنوان ترجیح شخصی، ستون را به یک هدف سری تبدیل می کنم تا از ارجاع به نام ستون ها، هر بار که از TS استفاده می کنم جلوگیری کنم. لطفا با خیال راحت از آن به عنوان یک دیتافریم استفاده کنید که برای شما عملکرد بهتری دارد.

ts = data[‘#Passengers’] ts.head(10)

قبل از ادامه، در مورد برخی از تکنیک های نمایه سازی برای داده های TS بحث خواهم کرد. بیایید با انتخاب یک مقدار خاص در هدف سری شروع کنیم. این کار به 2 روش زیر قابل انجام است:

 

#1. Specific the index as a string constant:

ts[‘1949-01-01’]

#2. Import the datetime library and use ‘datetime’ function:

from datetime import datetime

ts[datetime(1949,1,1)]

 

هر دو مقدار «112» را برمی‌گردانند که می‌ تواند از خروجی قبلی نیز تأیید شود. فرض کنید ما تمام داده ‌ها را تا می 1949 می ‌خواهیم. این کار را می ‌توان به دو روش انجام داد:

#1. Specify the entire range:

ts[‘1949-01-01′:’1949-05-01’]

#2. Use ‘:’ if one of the indices is at ends:

ts[:’1949-05-01′]

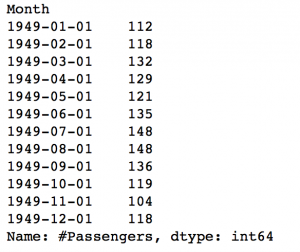
هر دو خروجی زیر را به دست خواهند آورد:

در اینجا 2 نکته قابل توجه است:

1. برخلاف نمایه سازی عددی، نمایه پایانی در اینجا گنجانده شده است. به عنوان مثال، اگر لیستی را به صورت [:5] نمایه کنیم، آنگاه مقادیر را در اندیس های – [0,1,2,3,4] برمی گرداند. اما در اینجا شاخص ‘1949-05-01’ در خروجی گنجانده شد.
2. شاخص ها باید مرتب شوند تا محدوده ها کار کنند. اگر به طور تصادفی شاخص را به هم بزنید، این روش کار نمی کند.

نمونه دیگری را در نظر بگیرید که در آن به تمام مقادیر سال 1949 نیاز دارید. این می تواند به صورت زیر انجام شود.

ts[‘1949’]

قسمت ماه حذف شد. به طور مشابه اگر تمام روز های یک ماه خاص را داشته باشید، قسمت روز را می توان حذف کرد.

حال اجازه دهید به تحلیل TS برویم.

 

3. چگونه ثابت بودن یک سری زمانی را بررسی کنیم؟

اگر ویژگی های آماری آن مانند میانگین، واریانس در طول زمان ثابت بماند، یک TS ثابت است. اما چرا مهم است؟ اکثر مدل های TS با این فرض کار می کنند که TS ثابت است. به طور شهودی، می توانیم بپذیریم که اگر یک TS در طول زمان رفتار خاصی داشته باشد، احتمال بسیار بالایی وجود دارد که در آینده نیز همین رفتار را داشته باشد. همچنین تئوری‌های مربوط به سری ‌های ثابت در مقایسه با سری‌ های غیر ساکن پخته ‌تر و آسان ‌تر اجرا می ‌شوند.

ثابت بودن با معیار بسیار دقیق تعریف می شود. با این حال، برای اهداف عملی می‌ توانیم این سری را ثابت فرض کنیم که دارای خواص آماری ثابت در طول زمان باشد، به عنوان مثال. به شرح زیر می باشد:

1. میانگین ثابت
2. واریانس ثابت
3. یک اتوکوواریانس که به زمان بستگی ندارد.

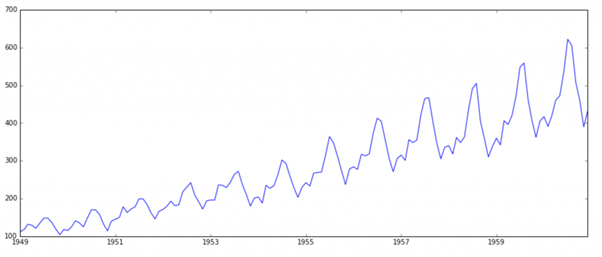
من از جزئیات صرف نظر می کنم زیرا در این مقاله بسیار واضح تعریف شده است. بیایید سراغ روش های آزمایش ثابت بودن برویم. اولین و مهمترین این است که داده ها را به صورت ساده رسم کنید و به صورت بصری تجزیه و تحلیل کنید. داده ها را می توان با استفاده از دستور زیر رسم کرد:

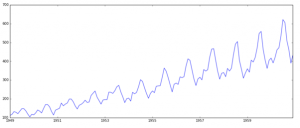
plt.plot(ts)

به وضوح مشهود است که یک روند افزایشی کلی در داده ها همراه با برخی تغییرات فصلی وجود دارد. با این حال، ممکن است همیشه نتوان چنین استنباط های بصری انجام داد (این موارد را بعدا مشاهده خواهیم کرد). بنابراین، به طور رسمی تر، می توانیم ثابت بودن را با استفاده از موارد زیر بررسی کنیم:

1. ترسیم آمار غلتشی یا چرخشی: می توانیم میانگین متحرک یا واریانس متحرک را رسم کنیم و ببینیم که آیا با زمان تغییر می کند یا خیر. منظور من از میانگین متحرک / واریانس این است که در هر لحظه ‘t’، میانگین / واریانس سال گذشته را می گیریم، یعنی 12 ماه گذشته اما باز هم این بیشتر یک تکنیک بصری است.
2. تست دیکی فولر: این یکی از آزمون های آماری برای بررسی ثابت بودن است. در اینجا فرضیه صفر این است که TS ثابت نیست. نتایج آزمون شامل یک آمار آزمون و مقداری بحرانی برای سطوح اطمینان تفاوت است. اگر «آمار آزمون» کمتر از «مقدار بحرانی» باشد، می‌توانیم فرضیه صفر را رد کنیم و بگوییم که سری ثابت است. برای جزئیات به این مقاله مراجعه کنید.

این مفاهیم ممکن است در این مرحله خیلی شهودی به نظر نرسند. توصیه می کنم مقاله پیش درآمد را مرور کنید. اگر به برخی از آمار های نظری علاقه مند هستید، می توانید به مقدمه سری های زمانی و پیش بینی نوشته براکول و دیویس مراجعه کنید. کتاب دارای کمی آمار سنگین است، اما اگر مهارت خواندن بین خطوط را داشته باشید، می توانید مفاهیم را درک کنید و به طور مماس آمار را لمس کنید.

برگردیم به بررسی ثابت بودن، ما از نمودار های آمار چرخشی همراه با نتایج آزمون دیکی فولر زیاد استفاده خواهیم کرد، بنابراین من تابعی را تعریف کرده ام که یک TS را به عنوان ورودی می گیرد و برای ما تولید می کند. لطفا توجه داشته باشید که من انحراف معیار را به جای واریانس ترسیم کرده ام تا واحد را مشابه میانگین نگه دارم.

from statsmodels.tsa.stattools import adfuller

def test_stationarity(timeseries):

    #Determing rolling statistics

    rolmean = pd.rolling_mean(timeseries, window=12)

    rolstd = pd.rolling_std(timeseries, window=12)

    #Plot rolling statistics:

    orig = plt.plot(timeseries, color=’blue’,label=’Original’)

    mean = plt.plot(rolmean, color=’red’, label=’Rolling Mean’)

    std = plt.plot(rolstd, color=’black’, label = ‘Rolling Std’)

    plt.legend(loc=’best’)

    plt.title(‘Rolling Mean & Standard Deviation’)

    plt.show(block=False)

    #Perform Dickey-Fuller test:

    print ‘Results of Dickey-Fuller Test:’

    dftest = adfuller(timeseries, autolag=’AIC’)

    dfoutput = pd.Series(dftest[0:4], index=[‘Test Statistic’,’p-value’,’#Lags Used’,’Number of Observations Used’])

    for key,value in dftest[4].items():

        dfoutput[‘Critical Value (%s)’%key] = value

    print dfoutput

کد بسیار واضح است. لطفا اگر در درک آن با مشکل مواجه شدید، در نظرات در مورد کد بحث کنید.

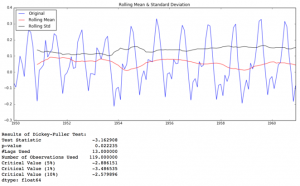
بیایید آن را برای سری ورودی خود اجرا کنیم:

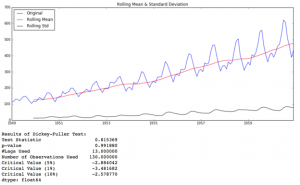
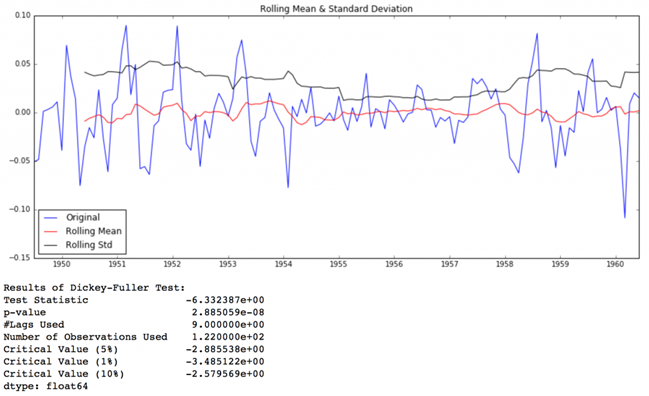
test_stationarity(ts)

اگرچه تغییرات در انحراف معیار کم است، اما میانگین به وضوح با گذشت زمان افزایش می یابد و این یک سری ثابت نیست. همچنین، آمار آزمون بسیار بیشتر از مقادیر بحرانی است. توجه داشته باشید که مقادیر علامت دار باید با هم مقایسه شوند نه مقادیر مطلق.

در مرحله بعد، در مورد تکنیک هایی که می توان از آنها برای هدایت این TS به سمت ثابت بودن استفاده کرد بحث خواهیم کرد.

 

4. چگونه یک سری زمانی را ثابت کنیم؟

اگر چه ثابت بودن فرض در بسیاری از مدل‌ های TS پذیرفته شده است، تقریبا هیچ یک از سری ‌های زمانی عملی ثابت نیستند. بنابراین آماردانان راه هایی را برای ثابت نگه داشتن سری ها پیدا کرده اند که اکنون در مورد آنها بحث خواهیم کرد. در واقع، تقریبا غیرممکن است که یک سریال را کاملا ثابت بسازیم، اما ما سعی می کنیم تا جایی که ممکن است آن را نزدیک کنیم.

بیایید بفهمیم که چه چیزی یک TS را ثابت نمی کند. 2 دلیل عمده پشت ثابت نبودن TS وجود دارد:

1. روند – متغیر میانگین در طول زمان. به عنوان مثال، در این مورد مشاهده کردیم که به طور متوسط ​​تعداد مسافران در طول زمان در حال افزایش است.
2. فصلی بودن – تغییرات در بازه های زمانی خاص. به عنوان مثال، ممکن است مردم به دلیل افزایش دستمزد یا جشنواره ها تمایل به خرید اتومبیل در یک ماه خاص داشته باشند.

اصل اساسی این است که روند و فصلی بودن سریال را مدل یا تخمین بزنیم و آن ‌ها را از سریال حذف کنیم تا یک سری ثابت به دست آوریم. سپس تکنیک های پیش بینی آماری را می توان بر روی این سری پیاده سازی کرد. مرحله نهایی تبدیل مقادیر پیش ‌بینی‌ شده به مقیاس اصلی با اعمال محدودیت ‌های روند و فصلی است.

توجه: من در مورد چند روش بحث خواهم کرد. برخی ممکن است در این مورد خوب کار کنند و برخی دیگر ممکن است عملکرد خوبی نداشته باشند. اما ایده اصلی این است که از همه روش ها استفاده کنید و فقط روی مشکل موجود تمرکز نکنید.

بیایید با کار روی بخش روند شروع کنیم.

برآورد و حذف روند

یکی از اولین ترفند ها برای کاهش روند می تواند دگرگونی باشد. به عنوان مثال، در این مورد به وضوح می توان مشاهده کرد که روند مثبت قابل توجهی وجود دارد. بنابراین می توانیم تبدیلی را اعمال کنیم که مقادیر بالاتر را بیشتر از مقادیر کوچکتر جریمه می کند. اینها می ‌توانند شامل گرفتن log، ریشه مربع، ریشه مکعب و غیره باشند. بیایید برای سادگی، یک تبدیل لگاریتم در اینجا بگیریم:

ts_log = np.log(ts)

plt.plot(ts_log)

در این حالت ساده تر، مشاهده روند رو به جلو در داده ها آسان است. اما در حضور نویز چندان شهودی نیست. بنابراین می ‌توانیم از تکنیک ‌هایی برای تخمین یا مدل ‌سازی این روند استفاده کنیم و سپس آن را از سری حذف کنیم. راه های زیادی برای انجام آن وجود دارد و برخی از رایج ترین آنها عبارتند از:

1. تجمیع – میانگین گرفتن برای یک دوره زمانی مانند میانگین های ماهانه / هفتگی
2. هموار سازی– گرفتن میانگین های غلط
3. برازش چند جمله ای – برازش یک مدل رگرسیون

من در اینجا در مورد هموار سازی صحبت خواهم کرد و شما باید تکنیک های دیگری را نیز امتحان کنید که ممکن است برای مشکلات دیگر جواب دهد. هموار سازی به تخمین های متحرک اشاره دارد، بدین معنی که با توجه به چند مورد گذشته راه های مختلفی می تواند وجود داشته باشد، اما من در اینجا به دو مورد از آنها خواهم پرداخت.

میانگین متحرک

در این رویکرد، بسته به فرکانس سری‌ های زمانی، میانگین مقادیر متوالی «k» را می ‌گیریم. در اینجا می توانیم میانگین 1 سال گذشته یا 12 مقدار آخر را در نظر بگیریم. پاندا ها عملکرد های خاصی برای تعیین آمار چرخشی دارند.

 

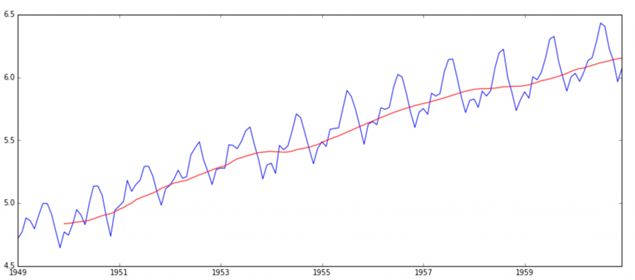
moving_avg = pd.rolling_mean(ts_log,12)

plt.plot(ts_log)

plt.plot(moving_avg, color=’red’)

خط قرمز میانگین نورد را نشان می دهد. اجازه دهید این را از سری اصلی کم کنیم. توجه داشته باشید که از آنجایی که ما میانگین 12 مقدار آخر را می گیریم، میانگین نورد برای 11 مقدار اول تعریف نشده است. این را می توان به صورت زیر مشاهده کرد:

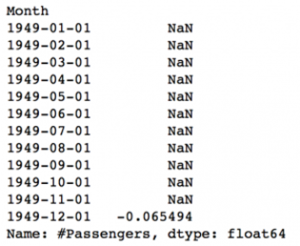
ts_log_moving_avg_diff = ts_log – moving_avg

ts_log_moving_avg_diff.head(12)

توجه کنید که 11 مورد اول Nan. هستند. اجازه دهید این مقادیر NaN را رها کرده و نمودار ها را برای آزمایش ثابت بودن بررسی کنیم.

ts_log_moving_avg_diff.dropna(inplace=True)

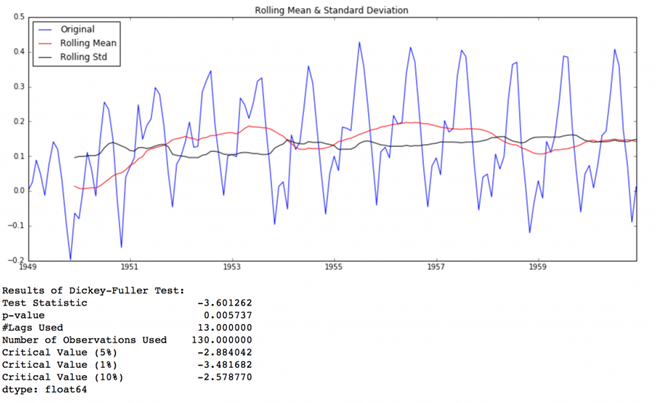
test_stationarity(ts_log_moving_avg_diff)

این سریال خیلی بهتر به نظر میرسد. به نظر می رسد که مقادیر نورد کمی متفاوت است اما روند خاصی وجود ندارد. همچنین، آمار آزمون کوچکتر از مقادیر بحرانی 5 درصد است، بنابراین می توان با اطمینان 95 درصد گفت که این یک سری ثابت است.

با این حال، یک اشکال در این رویکرد خاص این است که دوره زمانی باید کاملا تعریف شود. در این مورد، می‌توانیم میانگین ‌های سالانه را در نظر بگیریم، اما در موقعیت‌ های پیچیده مانند پیش ‌بینی قیمت سهام، رسیدن به عدد دشوار است. بنابراین ما یک «میانگین متحرک وزنی» می گیریم که در آن به مقادیر جدید تر وزن بیشتری داده می شود. تکنیک های زیادی برای تعیین وزن وجود دارد. یک مورد محبوب میانگین متحرک وزن‌ دار نمایی است که وزن ‌ها به تمام مقادیر قبلی با ضریب فروپاشی اختصاص داده می‌ شوند. جزئیات را در اینجا بیابید. این را می توان در پاندا ها به صورت زیر پیاده سازی کرد:

expwighted_avg = pd.ewma(ts_log, halflife=12)

plt.plot(ts_log)

plt.plot(expwighted_avg, color=’red’)

 

توجه داشته باشید که در اینجا از پارامتر “نیمه عمر یا halflife” برای تعریف میزان فروپاشی نمایی استفاده می شود. این در اینجا این فقط یک فرض است و تا حد زیادی به حوزه کسب و کار بستگی دارد. پارامتر های دیگری مانند دهانه span و مرکز جرم center of mass نیز می توانند برای تعریف فروپاشی استفاده شوند که در پیوند به اشتراک گذاشته شده در بالا مورد بحث قرار گرفته اند. حالا بیایید این را از سری حذف کنیم و ثابت بودن را بررسی کنیم:

ts_log_ewma_diff = ts_log – expwighted_avg

test_stationarity(ts_log_ewma_diff)

این TS دارای تغییرات کمتری در میانگین و انحراف معیار در بزرگی است. همچنین آمار آزمون از مقدار بحرانی 1% کوچکتر است که نسبت به حالت قبلی بهتر است. توجه داشته باشید که در این حالت هیچ مقدار گم شده ای وجود نخواهد داشت زیرا به همه مقادیر از شروع وزن داده می شود. بنابراین حتی بدون مقادیر قبلی نیز کار خواهد کرد.

 

حذف روند و فصلی بودن

تکنیک ‌های ساده کاهش روند که قبلا مورد بحث قرار گرفت، در همه موارد، به ‌ویژه مواردی که فصلی بودن زیاد دارند، کار نمی‌کنند. بیایید در مورد دو راه برای حذف روند و فصلی بودن بحث کنیم:

1. متمایز کردن – گرفتن تفاوت با یک تاخیر زمانی خاص
2. تجزیه – مدل سازی روند و فصلی بودن و حذف آنها از مدل.

متمایز کردن

یکی از متداول‌ ترین روش ‌های مقابله با روند و فصلی بودن، روش ‌های متمایز کردن است. در این تکنیک، تفاوت مشاهده در یک لحظه خاص را با آن در لحظه قبلی در نظر می گیریم. این بیشتر در بهبود ثابت بودن به خوبی عمل می کند. تفاوت مرتبه اول را می توان در پاندا ها به صورت زیر انجام داد:

()ts_log_diff = ts_log – ts_log.shift

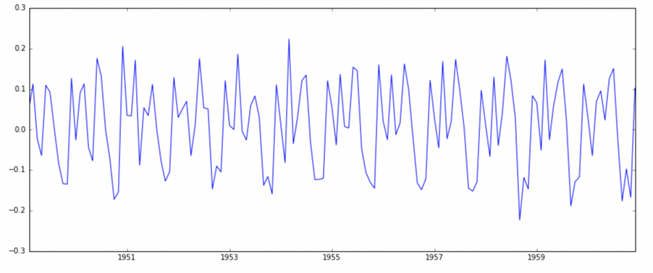
plt.plot(ts_log_diff)

به نظر می رسد که این، روند را به طور قابل توجهی کاهش داده است. بیایید با استفاده از نمودار های خود تأیید کنیم:

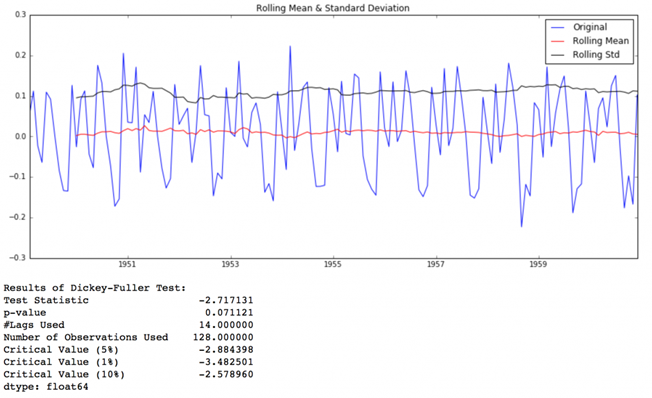
ts_log_diff.dropna(inplace=True)

test_stationarity(ts_log_diff)

می بینیم که تغییرات میانگین و std با زمان تغییرات کوچکی دارند. همچنین، آمار آزمون دیکی فولر کمتر از مقدار بحرانی 10 درصد است، بنابراین TS با اطمینان 90 درصد ثابت است. ما همچنین می ‌توانیم تفاوت‌ های مرتبه دوم یا سوم را انتخاب کنیم که ممکن است نتایج بهتری در برنامه ‌های خاص داشته باشد. این را به شما واگذار می کنم که آنها را امتحان کنید.

 

تجزیه شدن

در این رویکرد، هر دو روند و فصلی بودن به طور جداگانه مدل سازی شده و قسمت باقی مانده از سری برگردانده می شود. من از آمار می گذرم و به نتایج می رسم:

from statsmodels.tsa.seasonal import seasonal_decompose

decomposition = seasonal_decompose(ts_log)

trend = decomposition.trend

seasonal = decomposition.seasonal

residual = decomposition.resid

plt.subplot(411)

plt.plot(ts_log, label=’Original’)

plt.legend(loc=’best’)

plt.subplot(412)

plt.plot(trend, label=’Trend’)

plt.legend(loc=’best’)

plt.subplot(413)

plt.plot(seasonal,label=’Seasonality’)

plt.legend(loc=’best’)

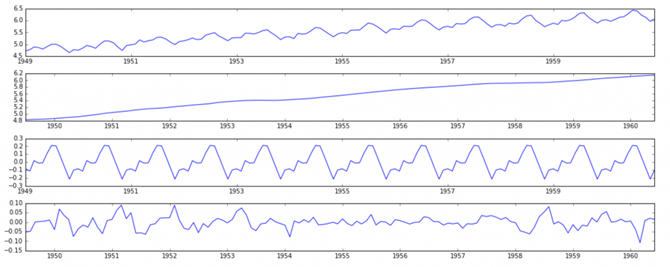
plt.subplot(414)

plt.plot(residual, label=’Residuals’)

plt.legend(loc=’best’)

plt.tight_layout()

در اینجا می بینیم که روند و فصلی بودن از داده ها جدا شده است و می توانیم باقیمانده ها را مدل سازی کنیم. بیایید ثابت بودن باقیمانده ها را بررسی کنیم:

ts_log_decompose = residual

ts_log_decompose.dropna(inplace=True)

test_stationarity(ts_log_decompose)

 

آمار آزمون دیکی فولر به طور قابل توجهی کمتر از مقدار بحرانی 1% است. بنابراین این TS بسیار نزدیک به ثابت است. می توانید تکنیک های تجزیه پیشرفته را نیز امتحان کنید که می تواند نتایج بهتری ایجاد کند. همچنین، باید توجه داشته باشید که تبدیل باقیمانده ها به مقادیر اصلی برای داده های آینده در این مورد چندان شهودی نیست.

 

5. پیش بینی یک سری زمانی

ما تکنیک های مختلفی را دیدیم و همه آنها برای ثابت کردن TS به خوبی کار کردند. بیایید پس از متمایز کردن، مدلی را روی TS بسازیم زیرا این یک تکنیک بسیار محبوب است. همچنین، اضافه کردن نویز و فصلی بودن به باقیمانده‌ های پیش‌ بینی‌ شده در این مورد نسبتا آسان ‌تر است. پس از انجام تکنیک های تخمین روند و فصلی بودن، دو حالت می تواند وجود داشته باشد:

1. یک سری کاملا ثابت و بدون وابستگی بین مقادیر. این مورد ساده ای است که در آن می توانیم باقی مانده ها را به عنوان نویز سفید مدل سازی کنیم. اما این بسیار نادر است.
2. مجموعه ای با وابستگی قابل توجه بین ارزش ها. در این مورد باید از برخی مدل های آماری مانند ARIMA برای پیش بینی داده ها استفاده کنیم.

اجازه دهید به شما معرفی مختصری از ARIMA بدهم. من وارد جزئیات فنی نمی ‌شوم، اما اگر می‌ خواهید آن‌ها را مؤثر تر به کار ببرید، باید این مفاهیم را با جزئیات درک کنید. ARIMA مخفف Auto Regressive Integrated Moving Averages است. پیش‌بینی ARIMA برای یک سری زمانی ثابت چیزی جز یک معادله خطی (مانند رگرسیون خطی) نیست. پیش بینی کننده ها به پارامتر های (p,d,q) مدل ARIMA بستگی دارند:

1. تعداد اصطلاحات AR (Auto Regressive) (p): اصطلاحات AR فقط تاخیر های متغیر وابسته هستند. برای مثال اگر p=5 باشد، پیش‌ بینی‌کننده ها برای ” x(t)‌ x(t-1)….x(t-5)” خواهند بود.
2. تعداد اصطلاحات MA (میانگین متحرک) (q): اصطلاحات MA خطا های پیش ‌بینی عقب افتاده در معادله پیش‌ بینی هستند. برای مثال اگر q برابر با 5 باشد، پیش‌ بینی‌کننده ها برای‌x(t) “e(t-1)….e(t-5)” خواهند بود. که در آن e(i) تفاوت بین میانگین متحرک در مقدار لحظه ای و واقعی i^th است.
3. تعداد تفاوت ها (d): اینها تعداد تفاوت های غیر فصلی هستند، یعنی در این مورد ما تفاوت مرتبه اول را گرفتیم. بنابراین یا می توانیم آن متغیر را پاس کرده و d=0 قرار دهیم یا متغیر اصلی را پاس کرده و d=1 قرار دهیم. هر دو نتایج یکسانی ایجاد خواهند کرد.

یک نگرانی مهم در اینجا این است که چگونه مقدار “p” و “q” را تعیین کنیم. برای تعیین این اعداد از دو نمودار استفاده می کنیم. بیایید ابتدا در مورد آنها بحث کنیم.

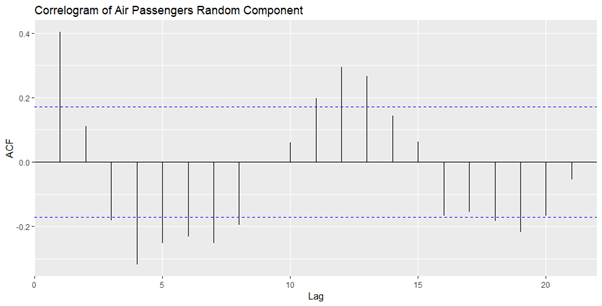
1. تابع همبستگی خودکار (ACF): این یک معیار برای همبستگی بین TS با یک نسخه عقب مانده از خودش است. به عنوان مثال در تاخیر 5، ACF سری در لحظه “t1″…’t2” را با سری در لحظه “t1-5″…”t2-5” مقایسه می کند (t1-5 و t2 نقاط پایانی هستند).
2. تابع خود همبستگی جزئی (PACF): این همبستگی بین TS را با یک نسخه عقب مانده از خود می سنجد، اما پس از حذف تغییراتی که قبلا توسط مقایسه های مداخله ای توضیح داده شده است. به عنوان مثال در تأخیر 5، همبستگی را بررسی می کند اما اثراتی که قبلا با تأخیر های 1 تا 4 توضیح داده شده را حذف می کند.

نمودار های ACF و PACF برای TS پس از تفاضل می توانند به صورت زیر ترسیم شوند.

 :ACF and PACF plot#

from statsmodels.tsa.stattools import acf, pacf

lag_acf = acf(ts_log_diff, nlags=20)

lag_pacf = pacf(ts_log_diff, nlags=20, method=’ols’)

#Plot ACF:

plt.subplot(121)

plt.plot(lag_acf)

plt.axhline(y=0,linestyle=’–‘,color=’gray’)

plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle=’–‘,color=’gray’)

plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle=’–‘,color=’gray’)

plt.title(‘Autocorrelation Function’)

#Plot PACF:

plt.subplot(122)

plt.plot(lag_pacf)

plt.axhline(y=0,linestyle=’–‘,color=’gray’)

plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle=’–‘,color=’gray’)

plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle=’–‘,color=’gray’)

plt.title(‘Partial Autocorrelation Function’)

plt.tight_layout()

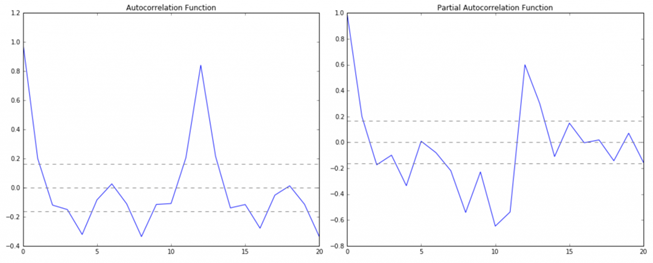
در این نمودار، دو خط نقطه چین در دو طرف 0، فواصل اطمینان هستند. اینها می توانند برای تعیین مقادیر “p” و “q” به صورت زیر استفاده شوند:

1. p – مقدار تاخیری که نمودار PACF برای اولین بار از فاصله اطمینان بالایی عبور می کند. اگر دقت کنید، در این مورد p=2 می باشد.
2. q – مقدار تاخیری که نمودار ACF برای اولین بار از فاصله اطمینان بالایی عبور می کند. اگر دقت کنید، در این مورد q=2 است.

اکنون، اجازه دهید 3 مدل مختلف ARIMA را با در نظر گرفتن تاثیر های فردی و ترکیبی بسازیم. من همچنین RSS را برای هر یک چاپ خواهم کرد. لطفا توجه داشته باشید که در اینجا RSS برای مقادیر باقیمانده است و نه سری واقعی.

ابتدا باید مدل ARIMA را بارگذاری کنیم:

from statsmodels.tsa.arima_model import ARIMA

مقادیر p,d,q را می توان با استفاده از آرگومان ترتیب ARIMA که یک دسته داده چندتایی یا tuple (p,d,q) می گیرد مشخص کرد. 3 مورد را مدل سازی کنید.

مدل AR

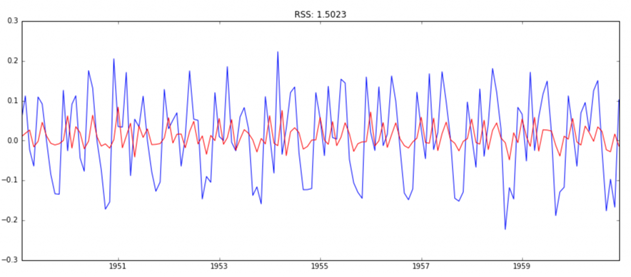
model = ARIMA(ts_log, order=(2, 1, 0))

results_AR = model.fit(disp=-1)

plt.plot(ts_log_diff)

plt.plot(results_AR.fittedvalues, color=’red’)

plt.title(‘RSS: %.4f’% sum((results_AR.fittedvalues-ts_log_diff)**2))

مدل MA

model = ARIMA(ts_log, order=(0, 1, 2))

results_MA = model.fit(disp=-1)

plt.plot(ts_log_diff)

plt.plot(results_MA.fittedvalues, color=’red’)

plt.title(‘RSS: %.4f’% sum((results_MA.fittedvalues-ts_log_diff)**2))

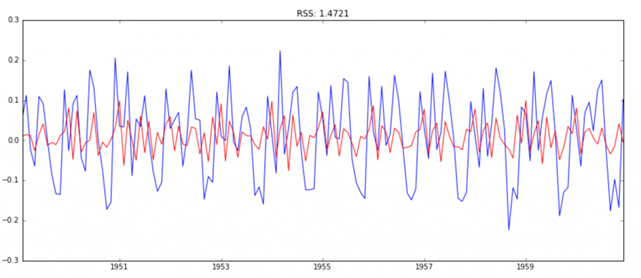
مدل ترکیبی

model = ARIMA(ts_log, order=(2, 1, 2))

results_ARIMA = model.fit(disp=-1)

plt.plot(ts_log_diff)

plt.plot(results_ARIMA.fittedvalues, color=’red’)

plt.title(‘RSS: %.4f’% sum((results_ARIMA.fittedvalues-ts_log_diff)**2))

در اینجا می ‌توانیم ببینیم که مدل‌های AR و MA تقریبا RSS یکسانی دارند، اما ترکیبی به طور قابل توجهی بهتر است. در حال حاضر، ما با 1 مرحله آخر، یعنی این مقادیر را به مقیاس اصلی برگردانید.

 

برگرداندن آن به مقیاس اصلی

از آنجایی که مدل ترکیبی بهترین نتیجه را داد، بیایید آن را به مقادیر اصلی برگردانیم و ببینیم که در آنجا چقدر خوب عمل می‌ کند. گام اول این است که نتایج پیش بینی شده را به صورت یک سری جداگانه ذخیره کرده و آن را مشاهده کنید.

predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True)

print predictions_ARIMA_diff.head()

توجه داشته باشید که این موارد از ‘1949-02-01’ شروع می شود و نه از ماه اول. چرا؟ این به این دلیل است که ما یک تاخیر توسط 1 گرفتیم و عنصر اول چیزی قبل از آن برای تفریق ندارد. روش تبدیل تفاضل به مقیاس log این است که این تفاوت ها را به صورت متوالی به عدد پایه اضافه کنید. یک راه آسان برای انجام آن این است که ابتدا مجموع تجمعی را در شاخص تعیین کنید و سپس آن را به عدد پایه اضافه کنید. مجموع تجمعی را می توان به صورت زیر یافت:

predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum()

print predictions_ARIMA_diff_cumsum.head()

شما می توانید به سرعت برخی از محاسبات را با استفاده از خروجی های قبلی انجام دهید تا بررسی کنید که آیا این محاسبات صحیح هستند یا خیر. سپس باید آنها را به شماره پایه اضافه کنیم. برای این کار اجازه می دهیم یک سری با تمام مقادیر به عنوان عدد پایه ایجاد کنیم و تفاوت ها را به آن اضافه کنیم. این کار را می توان به صورت زیر انجام داد:

predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum()

print predictions_ARIMA_diff_cumsum.head()

در اینجا اولین عنصر، خود عدد پایه است و از آن به بعد مقادیر به صورت تجمعی اضافه می شوند. مرحله آخر این است که نما را بگیرید و با سری اصلی مقایسه کنید.

predictions_ARIMA = np.exp(predictions_ARIMA_log)

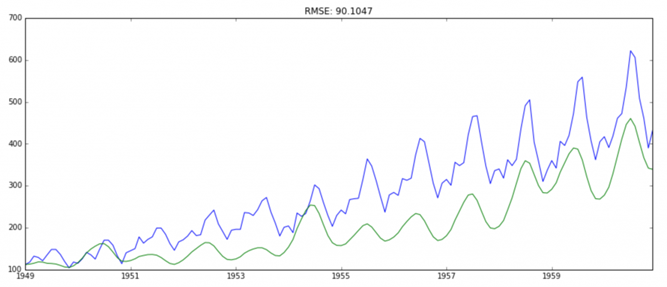
plt.plot(ts)

plt.plot(predictions_ARIMA)

plt.title(‘RMSE: %.4f’% np.sqrt(sum((predictions_ARIMA-ts)**2)/len(ts)))

همه اینها را در پایتون انجام دادیم. خوب، بیایید یاد بگیریم که چگونه یک پیش‌ بینی سری زمانی را در R پیاده‌ سازی کنیم.

پیش بینی سری زمانی در R

 مرحله 1: خواندن داده ها و محاسبه خلاصه اولیه

1 #Installing packages and calling out the libraries

2 install.packages(“summarytools”)

3 install.packages(“tseries”)

4 install.packages(“forecast”)

5 library(forecast)

6 library(ggplot2)

7 library(tseries)

8 library(summarytools)

9

10 #Reading the Airpaseengers data

11 data(“AirPassengers”)

12 tsdata<-AirPassengers

13 #Identifying the class of data

14 class(tsdata)

15 #Observations of the time series data

16 tsdata

17 #Summary of the data and missi

18 dfSummary(tsdata)

خروجی

class(tsdata)

“ts”

> #Observations of the time series data

> tsdata

Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec

1949 112 118 132 129 121 135 148 148 136 119 104 118

1950 115 126 141 135 125 149 170 170 158 133 114 140

1951 145 150 178 163 172 178 199 199 184 162 146 166

1952 171 180 193 181 183 218 230 242 209 191 172 194

1953 196 196 236 235 229 243 264 272 237 211 180 201

1954 204 188 235 227 234 264 302 293 259 229 203 229

1955 242 233 267 269 270 315 364 347 312 274 237 278

1956 284 277 317 313 318 374 413 405 355 306 271 306

1957 315 301 356 348 355 422 465 467 404 347 305 336

1958 340 318 362 348 363 435 491 505 404 359 310 337

1959 360 342 406 396 420 472 548 559 463 407 362 405

1960 417 391 419 461 472 535 622 606 508 461 390 432

> #Summary of the data and missi

tsdata was converted to a data frame

Data Frame Summary

tsdata

Dimensions: 144 x 1

Duplicates: 26

—————————————————————————————————-

No Variable Stats / Values Freqs (% of Valid) Graph Valid Missing

—- ———- ————————– ———————– ——————— ——– —

1 tsdata Mean (sd) : 280.3 (120) 118 distinct values . : . 144 0

[ts] min < med < max: Start: 1949-01 : : . . : (100%) (0%)

104 < 265.5 < 622 End : 1960-12 : : : : :

IQR (CV) : 180.5 (0.4) : : : : : : :

: : : : : : : : . .

—————————————————————————————————-

مرحله 2: بررسی چرخه داده های سری زمانی و رسم داده های خام

 Check the cycle of data and plot the raw data

  as.data.frame(tsdata)

 cycle(tsdata)

  plot(tsdata, ylab=”Passengers (1000s)”, type=”o”)

خروجی

cycle(tsdata)

Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec

1949 1 2 3 4 5 6 7 8 9 10 11 12

1950 1 2 3 4 5 6 7 8 9 10 11 12

1951 1 2 3 4 5 6 7 8 9 10 11 12

1952 1 2 3 4 5 6 7 8 9 10 11 12

1953 1 2 3 4 5 6 7 8 9 10 11 12

1954 1 2 3 4 5 6 7 8 9 10 11 12

1955 1 2 3 4 5 6 7 8 9 10 11 12

1956 1 2 3 4 5 6 7 8 9 10 11 12

1957 1 2 3 4 5 6 7 8 9 10 11 12

1958 1 2 3 4 5 6 7 8 9 10 11 12

1959 1 2 3 4 5 6 7 8 9 10 11 12

1960 1 2 3 4 5 6 7 8 9 10 11 12

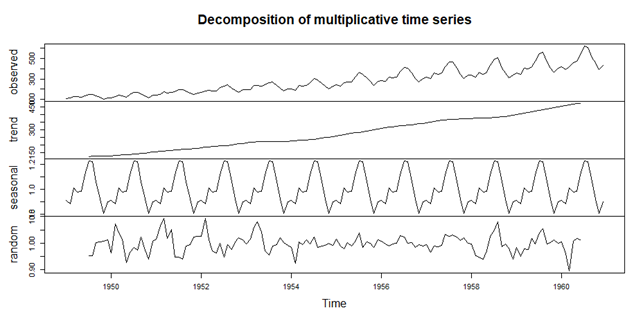
مرحله 3: تجزیه داده های سری زمانی

 Decomposing the data into its trend, seasonal, and random error components

 tsdata_decom <- decompose(tsdata, type = “multiplicative”)

  plot(tsdata_decom)

خروجی

مرحله 4: آزمایش ثابت بودن داده ها

 Testing the stationarity of the data

 Augmented Dickey-Fuller Test

  adf.test(tsdata)

خروجی

Augmented Dickey-Fuller Test

data: tsdata

Dickey-Fuller = -7.3186, Lag order = 5, p-value = 0.01

alternative hypothesis: stationary

مقدار p=0. 01 است که<0.05  است. بنابراین، ما فرضیه صفر را رد می کنیم و بنابراین سری زمانی ثابت است.

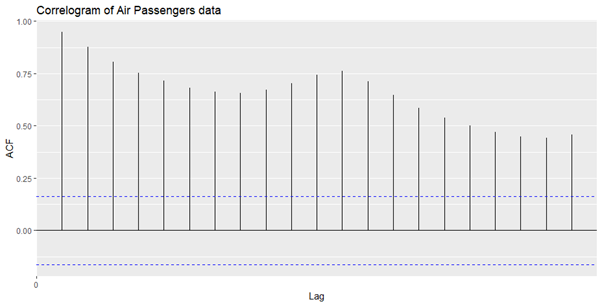
حداکثر تاخیر در 1 یا 12 ماه است، که نشان دهنده ارتباط مثبت با چرخه 12 ماهه است.

مشاهده های سری زمانی تصادفی را از 7:138 که مقادیر NA را حذف می کند، رسم خودکار کنید.

مرحله 5: برازش مدل

 Fitting the model

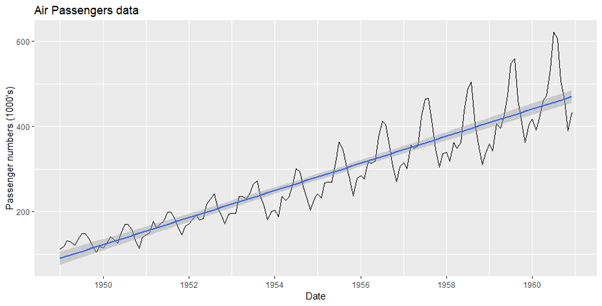
 Linear model

3 autoplot(tsdata) + geom_smooth(method=”lm”)+ labs(x =”Date”, y = “Passenger numbers 4 (1000’s)”, title=”Air Passengers data”)

5

 ARIMA Model

  arimats <- auto.arima(tsdata)

 arimats

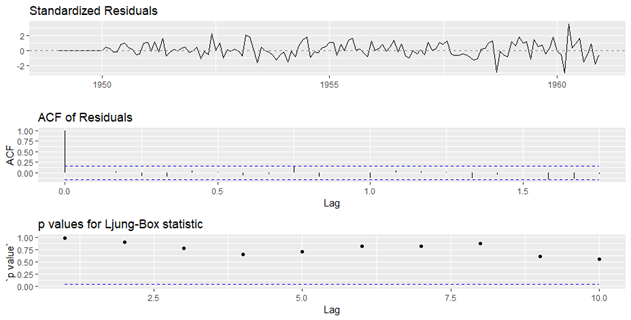
 ggtsdiag(arimats)

خروجی

 

Series: tsdata

ARIMA(2,1,1)(0,1,0)[12]

Coefficients:

ar1 ar2 ma1

0.5960 0.2143 -0.9819

s.e. 0.0888 0.0880 0.0292

sigma^2 estimated as 132.3: log likelihood=-504.92

AIC=1017.85 AICc=1018.17 BIC=1029.35

مرحله 6: پیش بینی

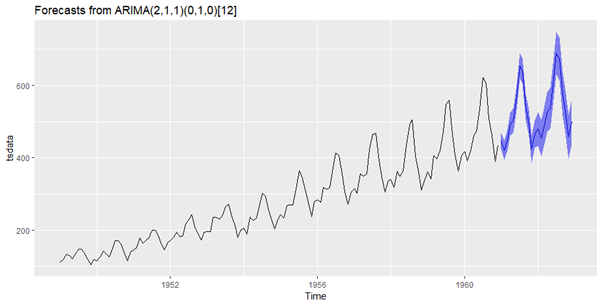
 Forecast of Arima Model

  fts <- forecast(arimats, level = c(95))

  autoplot(fts)

خروجی

در نهایت ما یک پیش بینی در مقیاس اصلی داریم. به نظر من پیش بینی خیلی خوبی نیست، اما شما این ایده را درست متوجه شدید؟ اکنون، این را به شما واگذار می کنم که روش شناسی را اصلاح کنید و راه حل بهتری ایجاد کنید./