رگریسیون خطی

مقدمه
به تجزیه و تحلیل پیش بینی کننده علاقه دارید؟ پس در مورد هوش مصنوعی، یادگیری ماشینی و یادگیری عمیق (deep learning) تحقیق کنید. اگر در مسیر یادگیری علم داده هستید، قطعا درک درستی از یادگیری ماشینی دارید. در دنیای دیجیتال امروزی، همه می دانند که یادگیری ماشینی چیست، زیرا این یک فناوری دیجیتال پرطرفدار در سراسر جهان می باشد.
در این مقاله ما فقط یادگیری ماشینی را مورد بحث قرار می دهیم، اگر نمی دانید چیست، مقدمه ای از یادگیری ماشینی را در ادامه آورده ایم: یادگیری ماشینی، مطالعه الگوریتم های رایانه ای است که به طور خودکار از طریق تجربه و با استفاده از داده ها بهبود می یابند. الگوریتم آن بر اساس داده هایی که در طول ساخت مدل ارائه می کنیم، یک مدل می سازد. این تعریف ساده یادگیری ماشینی است، وقتی بیشتر وارد موضوع می شویم، متوجه می شویم که تعداد زیادی الگوریتم وجود دارد که در ساخت مدل استفاده می شوند. به طور کلی، بیشتر الگوریتم های یادگیری ماشینی مورد استفاده بر اساس نوع مشکل یا مسئله هستند، انواع این مشکلات اساسا رگرسیون، طبقه بندی و غیره هستند…؛ اما در این جا فقط در مورد الگوریتم های رگرسیون صحبت خواهیم کرد.
مقدمه ای کوتاه در مورد این که رگرسیون چیست؟ رگرسیون روشی آماری در سرمایه گذاری، امور مالی و سایر رشته هاست که سعی در تعیین قدرت و رابطه بین متغیر های مستقل و وابسته دارد. به طور کلی متغیر های مستقل، آن دسته از متغیر هایی هستند که از مقادیر آن ها برای به دست آوردن خروجی استفاده می شود و متغیر های وابسته، آن دسته از متغیر هایی هستند که مقدار آن ها وابسته به مقادیر مستقل است. وقتی در مورد الگوریتم های رگرسیون صحبت می کنید، برخی از الگوریتم های رگرسیون که بیشتر مورد استفاده قرار می گیرند برای آموزش مدل یادگیری ماشینی استفاده می شوند، مانند رگرسیون خطی ساده، کمند (lasso)، برآمدگی (ridge) و غیره… .
بنابراین، بیایید در مورد رگرسیون خطی چندگانه صحبت کنیم و درک دقیقی از تفاوت سادگی رگرسیون خطی با رگرسیون خطی چندگانه داشته باشیم.
فهرست مطالب
- رگرسیون خطی ساده در مقابل رگرسیون خطی چندگانه
- مجموعه داده
- خواندن مجموعه داده
- متغیر های مستقل و وابسته
- مدیریت متغیر های طبقه بندی شده
- تقسیم داده ها
- اعمال مدل
رگرسیون خطی ساده در مقابل رگرسیون خطی چندگانه
اکنون، قبل از ادامه مبحث، اجازه دهید در مورد تعامل رگرسیون خطی ساده بحث کنیم، سپس سعی می کنیم رگرسیون خطی چندگانه و ساده را بر اساس آن شهودی که در واقع مشکل یادگیری ماشینی خود را حل می کنیم، مقایسه کنیم.
رگرسیون خطی ساده
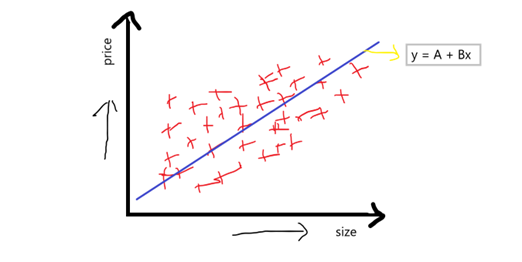
ما یک رگرسیون خطی ساده را در هر الگوریتم یادگیری ماشینی با استفاده از مثال در نظر گرفتیم، حال، فرض کنید اگر موردی از قیمت خانه را در نظر بگیریم که در آن محور x ما متراژ خانه است و محور y اساسا قیمت خانه است. در این موقعیت، ما اساسا دو ویژگی داریم که اولی f1 و دومی f2 است که
f1 به متراژ خانه و،
f2 به قیمت خانه اشاره دارد
بنابراین، اگر f1 تبدیل به ویژگی مستقل و f2 تبدیل به ویژگی وابسته شود، معمولا می دانیم که هر زمان متراژ خانه افزایش یابد، قیمت نیز افزایش می یابد، فرض کنید نقاط پراکندگی را به طور تصادفی ترسیم می کنیم، با این نقطه پراکندگی اساسا سعی می کنیم مناسب ترین خط را پیدا کنیم، و این مناسب ترین خط برازش با معادله زیر به دست می آید:
معادله: y = A + Bx
فرض کنید، y قیمت خانه و x متراژ خانه باشد، پس معادله به شکل زیر خواهد بود:
معادله: ) متراژ= A + B(قیمت
جایی که، A یک نقطه تلاقی (intercept)، و B شیب روی آن نقطه طلاقی است
وقتی این معادله را مورد بحث قرار می دهیم، که در آن به طور اساسی فاصله زمانی نشان می دهد که وقتی قیمت خانه 0 است، قیمت پایه خانه چقدر خواهد بود، و شیب یا ضریب نشان می دهد که با افزایش اندازه واحد، واحد در شیب چقدر افزایش خواهد یافت.
حال، رگرسیون خطی ساده در مقایسه با رگرسیون خطی چندگانه چه تفاوتی دارد؟
رگرسیون خطی چندگانه
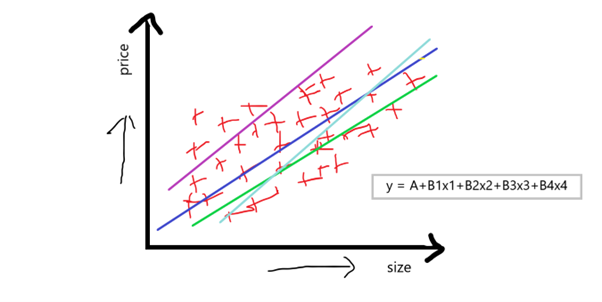
رگرسیون خطی چندگانه عمدتا نشان می دهد که ما ویژگی های زیادی مانند f1، f2، f3، f4 و ویژگی خروجی f5 خواهیم داشت. اگر همان مثالی را که در بالا بحث کردیم را در نظر بگیریم، فرض کنید:
f1 متراژ خانه،
f2 اتاق های نا مناسب خانه،
f3 محل خانه،
f4 وضعیت خانه،
و f5 ویژگی خروجی ما است که قیمت خانه می باشد.
اکنون، می بینید که چندین ویژگی مستقل نیز تأثیر زیادی بر قیمت خانه دارند، قیمت می تواند از یک ویژگی به ویژگی دیگر متفاوت باشد. وقتی در حال بحث از رگرسیون خطی چندگانه هستیم، معادله رگرسیون خطی ساده y = A + Bx به چیزی شبیه به معادله زیر تبدیل میشود:
معادله: y = A+B1x1+B2x2+B3x3+B4x4
“ما اگر یک ویژگی وابسته و چندین ویژگی مستقل داشته باشیم، اصولا آن را رگرسیون خطی چندگانه می نامیم.”
حال، هدف ما از استفاده از رگرسیون خطی چندگانه محاسبه A می باشد که یک نقطه تلاقی است، و B1 B2 B3 B4 را که شیب یا ضریب مربوط به این ویژگی مستقل هستند، که عمدتا نشانگر این است که اگر مقدار x1 را 1 واحد افزایش دهیم، سپس B1 می گوید که این کار چه مقدار بر قیمت خانه تأثیر می گذارد، و این عمل در مورد B2 B3 B4 نیز مشابه می باشد.
بنابراین، این یک توصیف نظری کوچک از رگرسیون خطی چندگانه است، اکنون ما از کتابخانه رگرسیون خطی learn scikit برای حل مسئله رگرسیون خطی چندگانه استفاده خواهیم کرد. مجموعه داده
اکنون، رگرسیون خطی چندگانه را روی مجموعه داده 50_startups اعمال می کنیم، برای دانلود مجموعه داده می توانید اینجا کلیک کنید.
خواندن مجموعه داده
اکثر مجموعه داده ها در قالب فایل CSV هستند، برای خواندن این فایل از کتابخانه pandas استفاده خواهیم کرد:
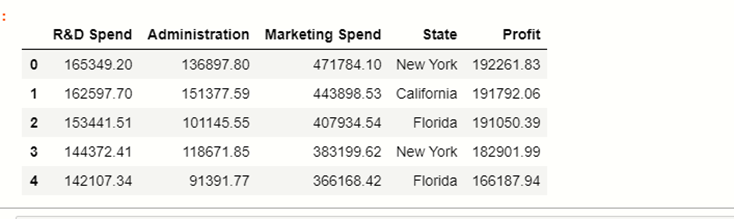
df = pd.read_csv(’50_Startups.csv’)
df
در اینجا مشاهده می کنید که 5 ستون در مجموعه داده وجود دارد که آن حالت، نقاط داده طبقه بندی شده را ذخیره می کند و بقیه ویژگی های عددی هستند. حال باید ویژگی های مستقل و وابسته را طبقه بندی کنیم:
متغیرهای مستقل و وابسته
در مجموع 5 ویژگی در مجموعه داده وجود دارد که در آن ها سود ما عمدتا ویژگی وابسته است و بقیه آنها ویژگی های مستقل ما هستند:
#separate the other attributes from the predicting attribute
x = df.drop(‘Profit’,axis=1)
#separte the predicting attribute into Y for model training
y = [‘profit’]
مدیریت متغیر های طبقه بندی شده
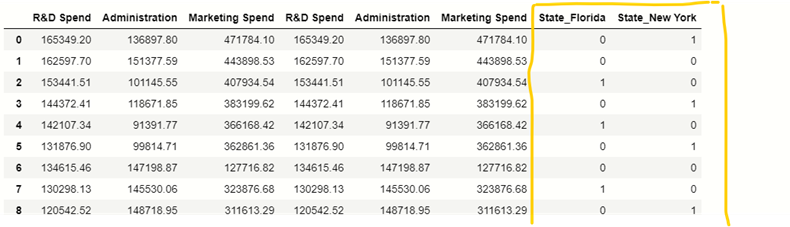
در مجموعه داده ما، یک ستون حالت طبقه بندی شده وجود دارد، ما باید این مقادیر طبقه بندی شده موجود در این ستون را مدیریت کنیم برای این کار از تابع get_dummies() pandas استفاده می کنیم:
# handle categorical variable
states=pd.get_dummies(x,drop_first=True)
# dropping extra column
x= x.drop(‘State’,axis=1)
# concatation of independent variables and new cateorical variable.
x=pd.concat([x,states],axis=1)
x
تقسیم داده ها
اکنون، ما باید داده ها را به بخش های آموزشی و آزمایشی تقسیم کنیم تا از تابع “train_test_split()” scikit-learnاستفاده کنیم.
# importing train_test_split from sklearn
from sklearn.model_selection import train_test_split
# splitting the data
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state = 42)
اعمال مدل
اکنون، ما مدل رگرسیون خطی را برای داده های آموزشی خود اعمال می کنیم. ابتدا، باید رگرسیون خطی را از کتابخانه scikit-learn وارد کنیم، کتابخانه دیگری برای اجرای رگرسیون خطی چندگانه وجود ندارد؛ پس ما آن را فقط با رگرسیون خطی انجام می دهیم.
# importing module
from sklearn.linear_model import LinearRegression
# creating an object of LinearRegression class
LR = LinearRegression()
# fitting the training data
LR.fit(x_train,y_train)
در نهایت، اگر این کد را اجرا کنیم، مدل ما آماده خواهد شد، اکنون داده های x_test را در اختیار داریم که از این داده ها برای پیش بینی سود استفاده می کنیم.
y_prediction = LR.predict(x_test)
y_prediction
حال باید مقادیر y_prediction را با مقادیر اصلی مقایسه کنیم زیرا باید دقت مدل خود را محاسبه کنیم، که توسط مفهومی به نام r2_score پیاده سازی شده است. بیایید به طور خلاصه در مورد r2_score بحث کنیم:
r2_score: – این یک تابع در داخل sklearn است. ماژول متریک، که در آن مقدار r2_score بین 0 تا 100 درصد متغیر است، می توان گفت که ارتباط نزدیکی با MSE دارد.
r2 اساسا با فرمول زیر محاسبه می شود:
فرمول: r2 = 1 – (SSres /SSmean )
حالا وقتی میگوییم SSres یعنی مجموع باقی مانده ها و SSmean به مجموع میانگین ها اشاره دارد.
جایی که،
y = مقادیر اصلی
^y = مقادیر پیش بینی شده. و،
اگر محاسبه را از این معادله بگیریم، باید بدانیم که مقدار مجموع میانگین ها همیشه از مجموع باقی مانده ها بیشتر است. اگر این شرط برآورده شود، مدل ما برای پیش بینی مناسب می باشد. مقادیر آن بین 0.0 تا 1 می باشد.
“نسبت واریانس در متغیر وابسته که از متغیر(های) مستقل قابل پیش بینی است.”
بهترین امتیاز ممکن 1.0 است و می تواند منفی باشد زیرا مدل می تواند به طور اختیاری بدتر باشد. یک مدل ثابت که همیشه مقدار مورد انتظار y را پیش بینی می کند، بدون توجه به ویژگی های ورودی، امتیاز “R2” 0.0 را دریافت می کند.
# importing r2_score module
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
# predicting the accuracy score
score=r2_score(y_test,y_prediction)
print(‘r2 socre is ‘,score)
print(‘mean_sqrd_error is==’,mean_squared_error(y_test,y_prediction))
print(‘root_mean_squared error of is==’,np.sqrt(mean_squared_error(y_test,y_prediction)))
می بینید که امتیاز دقت بیشتر از 0.8 است یعنی می توانیم از این مدل برای حل رگرسیون خطی چندگانه استفاده کنیم و همچنین میانگین نرخ مربعات خطا نیز کم است./

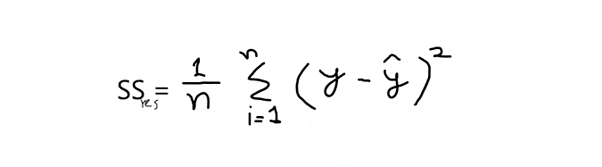
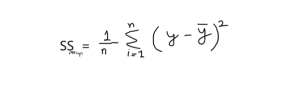

دیدگاهتان را بنویسید