داده های پرت 2

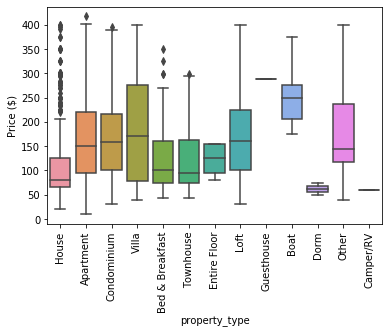
تشخیص پرت در تحلیل رگرسیون

استفاده از فاصله کوک (Cook’s Distance) در Scikit Learn و Statsmodel برای تشخیص رگرسیون پرت

 

مقدمه

نقاط پرت به عنوان مقادیر غیر عادی در یک مجموعه داده تعریف می شوند که با توزیع منظم مطابقت ندارند و این پتانسیل را دارند که به طور قابل توجهی هر مدل رگرسیونی را تحریف کنند. بنابراین، برای به دست آوردن بینش درست از داده ها، باید به دقت رفتار شود. معمولا داده‌ های جمع ‌آوری ‌شده از دنیای واقعی شامل چندین مشاهدات در چندین ویژگی است و بسیاری از مقادیر ممکن است به اشتباه قرار داده شوند یا به سادگی ممکن است به صورت مصنوع پردازش داده شده باشند. دلیل پرت بودن نقاط هر چه باشد، باید آن ‌ها را تحلیل کرد و واقعی بودن آن ‌ها را تأیید کرد. اگر نقاط پرت واقعی باشند، می توان آن را در یک مدل رگرسیونی قرار داد یا به سادگی آنها را رها کرد تا مدل رگرسیونی بهتری ساخت.

مجموعه داده

به منظور پیاده سازی در پایتون، من از رگرسیون خطی Scikit Learn و روش OLS Statsmodel برای بدست آوردن داده های قیمت مسکن استفاده می کنم. برای سادگی، تمام داده های ویژگی های گرفته شده در اینجا عددی هستند. من از همان داده های قیمت مسکن که در مقاله زیر استفاده شده است استفاده خواهم کرد.

من با مدل رگرسیون خطی برای قیمت مسکن با چندین پیش بینی عددی از مجموعه داده شروع خواهم کرد. پیش بینی کننده ها عبارتند از “OverallQual”، “GrLivArea”، “TotalBsmtSF”، “YearBuilt”، “FullBath”، “HalfBath”، “GarageArea” و هدف “SalePrice” است. توضیحات مربوط به این ویژگی ها در زیر آمده است.

‘OverallQual’: ‘Overall material and finish of the house’
‘GrLivArea’: ‘Ground living area square feet’
‘TotalBsmtSF’: ‘Total square feet of basement area
‘YearBuilt’: ‘Original construction date’
‘FullBath’: ‘Full bathrooms above grade’
‘HalfBath’: ‘Half baths above grade’
‘GarageArea’: ‘Size of garage in square feet’

من همچنین مقاله دیگری برای تشخیص نقاط پرت دارم که به ویژه بر روی اعداد پرت مبتنی بر روش‌های IQR، Hampel و DBSCAN تمرکز دارد.

https://towardsdatascience.com/practical-implementation-of-outlier-detection-in-python-90680453b3ce

این مقاله مختص به مدل رگرسیون و استفاده از روش فاصله کوک برای تشخیص نقاط پرت خواهد بود.

Scikit-Learn و Statsmodel

ما علاقه مندیم که کیفیت برازش بین Scikit-Learn و Statsmodel را بررسی کنیم. ابتدا، مدل رگرسیون خطی Scikit-Learn بر روی پیش ‌بینی‌کننده‌ ها و متغیر هدف برازش داده شد.

 

	1 house_df = pd.read_csv(‘house_prices_dataset.csv’)
	2 predictors = [‘OverallQual’, ‘GrLivArea’, ‘TotalBsmtSF’,
	3               ‘YearBuilt’, ‘FullBath’,    ‘HalfBath’, ‘GarageArea’]
	4 target = ‘SalePrice’
	5 house_lm = LinearRegression()
	6 house_lm.fit(house_df[predictors], house_df[target])
	7
	8 print(f’Intercept: {house_lm.intercept_:.3f}’)
	9 print(‘Coefficients:’)
	10 for name, coef in zip(predictors, house_lm.coef_):
	11     print(f’ {name}: {coef}’)

1 fitted = house_lm.predict(X_df[predictors])

2 RMSE = np.sqrt(mean_squared_error(X_df[target], fitted))

3 r2 = r2_score(X_df[target], fitted)

4 print(f’RMSE: {RMSE:.0f}’)

5 print(f’r2: {r2:.4f}’)

مقدار مربع R به دست آمده توسط این مدل 0.7672 است که اساسا نشان می دهد که تقریباً. 76٪ از واریانس در مجموعه داده توسط پیش بینی هایی که ما انتخاب کرده ایم توضیح داده شده است.

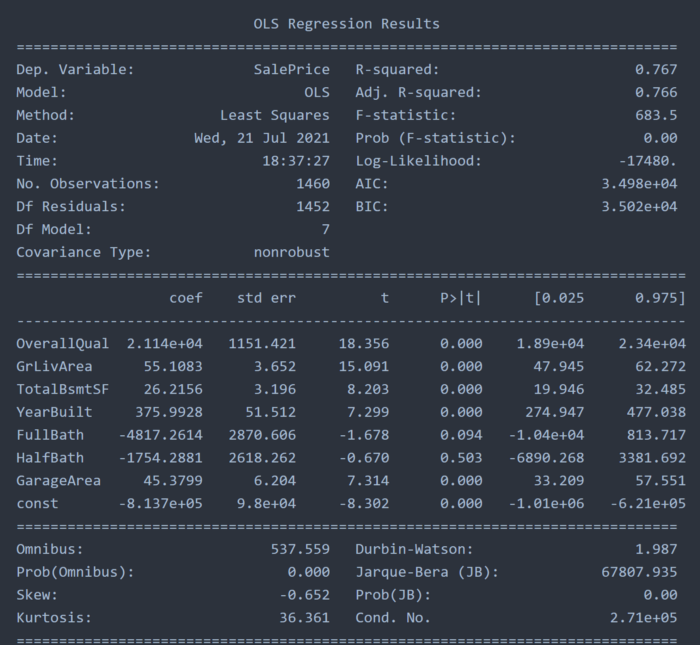
وقتی به Statsmodel تغییر دهید، مقدار مربع R تقریباً مشابه 0.767 باقی می‌ ماند و کاربر همچنین می ‌تواند مربع R تنظیم ‌شده را انتخاب کند که در این مورد با آن تفاوتی ندارد که نشان‌ دهنده تناسب خوبی برای ویژگی ‌های انتخاب شده در ابتدا است.

 

1 model = sm.OLS(X_df[target], X_df[predictors].assign(const=1))

2 results = model.fit()

3 print(results.summary())

4

تجزیه و تحلیل پرت

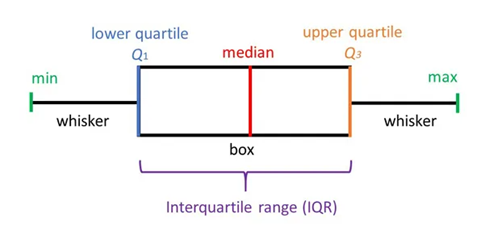
OLSinfluence Statmodel راهی سریع برای اندازه گیری تأثیر هر مشاهدات ارائه می دهد. هنگامی که داده ها در نمودار های جعبه ای رسم می شوند، تجزیه و تحلیل پرت کلی بر روی داده ها و نقاطی که بالاتر یا کمتر از 1.5 هستند انجام می شود.

تصویر از  simplypsychology.org

آن نقاط پرت گاهی بسیار زیاد یا بسیار کم هستند و می توانند خوشه های محلی را تشکیل دهند. اگر نمودار های جعبه ای سنتی را انتخاب کنیم، خوشه های محلی به عنوان نقاط پرت شناسایی می شوند. روش ‌های دیگر مانند DBSCAN می ‌توانند به طور موثر آن نقاط انتهایی را شناسایی کنند و می ‌توانند آن‌ ها را در تجزیه و تحلیل بگنجانند زیرا از الگوریتم مبتنی بر چگالی پیروی می ‌کنند.

با این حال، در رگرسیون، باقیمانده استاندارد شده یک شاخص برای نقاط پرت است. این کار نقطه داده را از نظر اینکه خطای استاندارد چقدر از خط رگرسیون فاصله دارد را  اندازه گیری می کند. ما از این باقیمانده برای همان مجموعه داده استفاده خواهیم کرد.

1 influence = OLSInfluence(results)

2 sresiduals = influence.resid_studentized_internal

3 print(sresiduals.idxmin(), sresiduals.min())

4

5 outlier = X_df.loc[sresiduals.idxmin(), :]

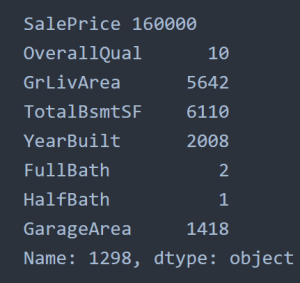
6 print(‘SalePrice’, outlier[target])

7 print(outlier[predictors])

در اینجا، ما می توانیم تأثیر گذارترین نقطه داده را در خط رگرسیون ببینیم که اساسا یک نقطه منفرد است که بالا ترین قدرت را برای کنترل مدل دارد.

قطعا بسته به موارد متفاوت، می توان آن را حفظ کرد یا آن را رها کرد. در بلوک کد زیر می توانیم تأثیرات همه نقاط را رسم کنیم. هنگامی که با plotly express نمودار ترسیم می شود، تشخیص نقاط پرت حتی با بالا و پایین کردن آنها آسان تر است.

1 data = pd.DataFrame(columns = [‘Id’, ‘X’, ‘Y’, ‘YearBuilt’, ‘OverallQual’,’Dist’])

2 data[‘Id’] = X_df.Id

3 data[‘X’] = influence.hat_matrix_diag

4 data[‘Y’] = influence.resid_studentized_internal

5 data[‘YearBuilt’] = X_df[“YearBuilt”]

6 data[‘Dist’] = influence.cooks_distance[0]

7 fig = px.scatter(data, x=’X’, y=’Y’, hover_data = [“Id”,”YearBuilt”])

8 fig.show()

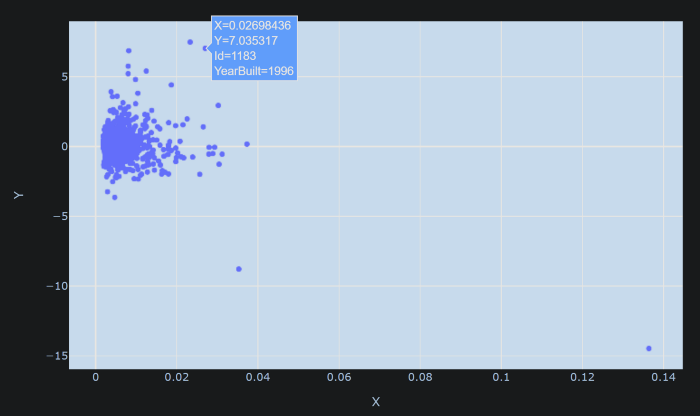
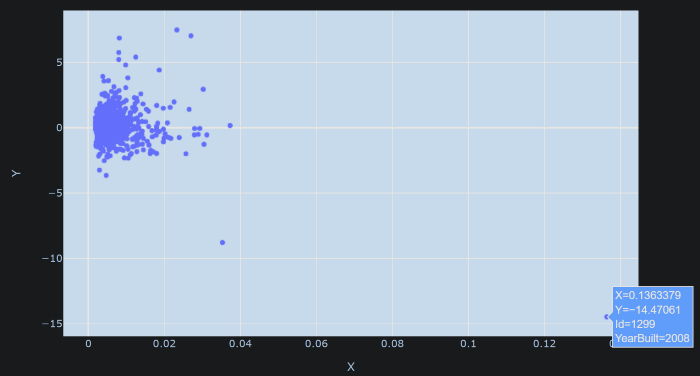
محور X مقادیر کلاه (hat values) را برای نقاط داده نشان می دهد. رگرسیون خطی چندگانه به صورت زیر بیان می شود

Y = HX

که در آن Y نتیجه با X به عنوان پیش بینی کننده است. H ماتریس کلاه و مقادیر کلاه اجزای مورب ماتریس H هستند. محور Y نشان دهنده باقیمانده های استاندارد شده است. بدیهی است که سمت راست ترین نقطه یک نقطه پرت با ارزش کلاه بسیار بالا است. داده های شناور را می توان برای نمایش اطلاعات بیشتر در مورد آن تغییر داد.

در این مرحله، فاصله کوک را معرفی می کنیم که معیاری برای اندازه گیری تأثیر نقاط داده است. فاصله کوک ترکیبی از اهرم (تعریف ویکیپدیا: در آمار و به ویژه در تجزیه و تحلیل رگرسیون، اهرم معیاری است از فاصله مقادیر متغیر مستقل مشاهدات از سایر مشاهدات) و اندازه باقیمانده.

1 import plotly.graph_objs as go

2 from plotly.offline import iplot, init_notebook_mode

3 import cufflinks

4

5 cufflinks.go_offline(connected=True)

6 init_notebook_mode(connected=True)

7 import pandas as pd

8 from sklearn.datasets import load_boston

9

10 data.iplot(

11     x=’X’,

12     y=’Y’,

13     size=data[‘Dist’]*10,

14     text=’Dist’,

15     mode=’markers’,

16     layout=dict(

17         xaxis=dict(title=’Id’),

18         yaxis=dict(title=’Studentized residuals’),

19         title=”Id vs Studentized residuals sized by Cook’s Distance”))

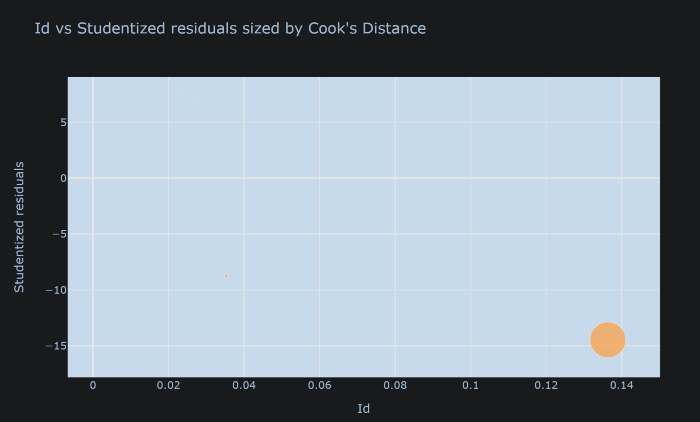
هنگامی که به این شکل ترسیم می شود، آن نقطه به قدری تأثیر می گذارد که سهم همه نقاط دیگر به سختی قابل توجه است.

ما باید فاصله کوک را کاهش دهیم تا متوجه دیگران شویم. وقتی 50 مقیاس بندی می شود، سایر نکات به تصویر بزرگ می رسند.

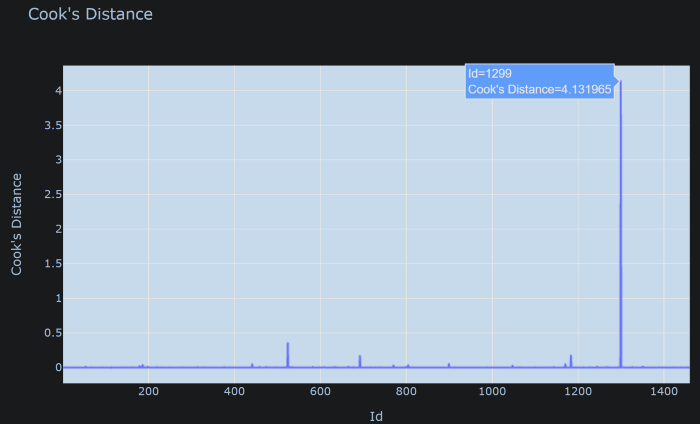
ترسیم فاصله کوک

فاصله کوک مشتق شده از نقاط داده است و از نمونه ای به نمونه دیگر متفاوت است. بلوک زیر فاصله کوک را به شکلی که به راحتی قابل شناسایی است برای تشخیص نقاط پرت ترسیم می کند. در اینجا، ما Id را روی محور X قرار دادیم.

1 influence = OLSInfluence(house_outlier)

2 C = influence.cooks_distance[0]

3

4 Cook = pd.DataFrame(columns = [‘Id’, “Cook_’s Distance”])

5 Cook[‘Id’] = X_df.Id

6 Cook[“Cook’s Distance”] = C

7 fig = px.line(Cook, x=”Id”, y=”Cook’s Distance”, title = “Cook’s Distance”)

8 fig.show()

در این مورد می‌توان آن نقطه تأثیرگذار را رها کرد و با مدل رگرسیون ادامه داد، زیرا قدرت زیادی برای تحریف مدل دارد.

نتیجه گیری

در این مقاله، استفاده از Scikit-Learn و Stasmodel را برای ارزیابی مدل رگرسیون نشان داده ‌ایم. بعدا با استفاده از Stasmodel، نقاط پرت بر اساس فاصله کوک شناسایی می شوند. داده های دنیای واقعی ممکن است به دلیل خطای انسانی دارای چندین نقطه پرت باشند یا ممکن است به عنوان مصنوعات تجزیه و تحلیل تولید شوند. بسته به مورد، تحلیلگر / دانشمند داده ممکن است تصمیم بگیرد که مقادیر پرت را حفظ یا حذف کند./