انتخاب ویژگی و همبستگی 2
تجزیه و تحلیل مؤلفه اصلی برای تصویر سازی
تجزیه و تحلیل اجزای اصلی (PCA) یک تکنیک یادگیری ماشینی بدون نظارت است. شاید محبوب ترین استفاده از تحلیل مؤلفه اصلی، کاهش ابعاد باشد. علاوه بر استفاده از PCA به عنوان یک تکنیک آماده سازی داده، می توانیم از آن برای کمک به تجسم داده ها نیز استفاده کنیم. یک تصویر ارزشمند تر از هزار کلمه است. با تجسم دادهها، دریافت برخی از دیدگاه ها و تصمیم گیری در مورد مرحله بعدی در مدل های یادگیری ماشینی برای ما آسان تر است.
در این آموزش، نحوه تجسم داده ها با استفاده از PCA و همچنین طرز استفاده از تصویر سازی برای کمک به تعیین پارامتر برای کاهش ابعاد را خواهید یافت.
پس از تکمیل این آموزش، خواهید دانست:
- نحوه استفاده از تصویر سازی داده با ابعاد بالا
- واریانس توضیح داده شده در PCA چیست
- واریانس توضیح داده شده از نتیجه PCA را با داده های با ابعاد بالا را به صورت بصری مشاهده کنید
بیایید شروع کنیم.
بررسی کلی این مقاله آموزشی
این آموزش به دو بخش تقسیم می شود؛ که شامل:
- نمودار پراکندگی (ترسیم پراکنده یا ترسیم توزیعی) داده ها با ابعاد بالا
- تصویر سازی یا تجسم واریانس توضیح داده شده
پیش نیاز ها
برای این آموزش، فرض می کنیم که شما با موارد زیر آشنا هستید:
- نحوه محاسبه تجزیه و تحلیل اجزای اصلی (PCA) از ابتدا در پایتون
- تجزیه و تحلیل مؤلفه اصلی برای کاهش ابعاد در پایتون
نمودار پراکندگی داده ها با ابعاد بالا
تجسم گامی مهم برای به دست آوردن دیدگاهی از داده ها می باشد. ما می توانیم با استفاده از تجسم بفهمیم که آیا می توان یک الگو را مشاهده کرد و از این رو تخمین زد که کدام مدل یادگیری ماشینی مناسب است.
به راحتی می توان چیز ها را در دو بعدی به تصویر کشید. به طور معمول نمودار پراکندگی با محور x و y دو بعدی است. به تصویر کشیدن چیز ها به صورت سه بعدی کمی چالش برانگیز است اما غیر ممکن نیست. به عنوان مثال، در matplotlib، می توانید به صورت سه بعدی رسم کنید. تنها مشکل تجسم سه بعدی روی کاغذ یا روی صفحه است، ما فقط میتوانیم در هر بار به یک نمودار سه بعدی در یک نما یا تجسم نگاه کنیم. در matplotlib، این با درجه ارتفاع و آزیموت (Azimuth) کنترل می شود. به تصویر کشیدن چیز ها در چهار یا پنج بعد غیر ممکن است زیرا ما در یک دنیای سه بعدی زندگی می کنیم و هیچ ایده ای از این که چیز ها در چنین بعد بالایی چگونه به نظر می رسند، نداریم.
اینجا ست که تکنیک کاهش ابعاد مانند PCA وارد عمل می شود. می توانیم بعد را به دو یا سه کاهش دهیم تا بتوانیم آن را تجسم کنیم. بیایید با یک مثال شروع کنیم. ما با مجموعه داده واین (wine dataset) شروع می کنیم، که یک مجموعه داده طبقه بندی شده با 13 ویژگی (یعنی مجموعه داده 13 بعدی است) و 3 کلاس می باشد. 178 نمونه وجود دارد:
|
1. from sklearn.datasets import load_wine |
| 2. winedata = load_wine() |
| 3. X, y = winedata[‘data’], winedata[‘target’] |
| 4. print(X.shape) |
| 5. print(y.shape) |
|
1. (178, 13) |
| 2. (178,) |
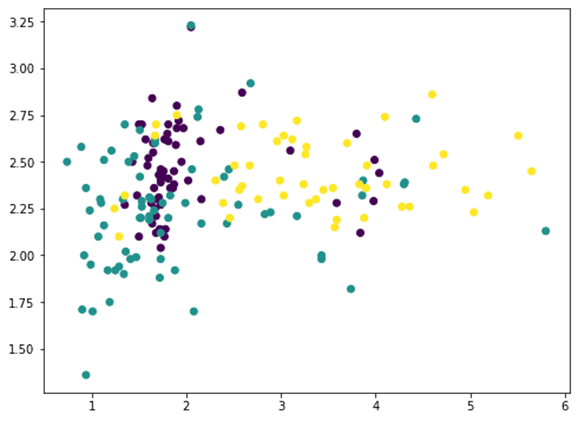
از میان 13 ویژگی، میتوانیم دو ویژگی را انتخاب کنیم و با matplotlib رسم کنیم (کلاس های مختلف با استفاده از آرگومان (شناسه) c کد رنگی گذاشته شده است):
|
1. … |
| 2. import matplotlib.pyplot as plt |
| 3. plt.scatter(X[:,1], X[:,2], c=y) |
| 4. plt.show() |
|
1. … |
| 2. ax = fig.add_subplot(projection=’3d’) |
| 3. ax.scatter(X[:,1], X[:,2], X[:,3], c=y) |
| 4. plt.show() |
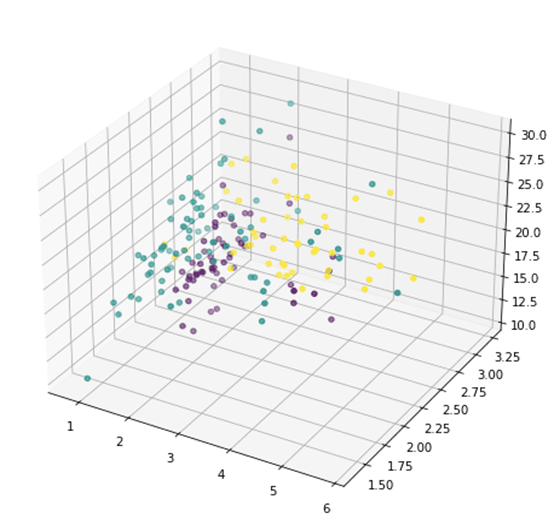
یا می توانیم سه مورد را به صورت دلخواه انتخاب کرده و به صورت سه بعدی نشان دهیم:
|
1. … |
| 2. ax = fig.add_subplot(projection=’3d’) |
| 3. ax.scatter(X[:,1], X[:,2], X[:,3], c=y) |
| 4. plt.show() |
اما این چیز زیادی از ظاهر داده ها نشان نمی دهد، زیرا اکثر ویژگی ها نشان داده نمی شوند. اکنون به تحلیل مؤلفه های اصلی روی می آوریم:
|
1. … |
| 2. from sklearn.decomposition import PCA |
| 3. pca = PCA() |
| 4. Xt = pca.fit_transform(X) |
| 5. plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) |
| 6. plt.legend(handles=plot.legend_elements()[0], labels=list(winedata[‘target_names’])) |
| 7. plt.show() |
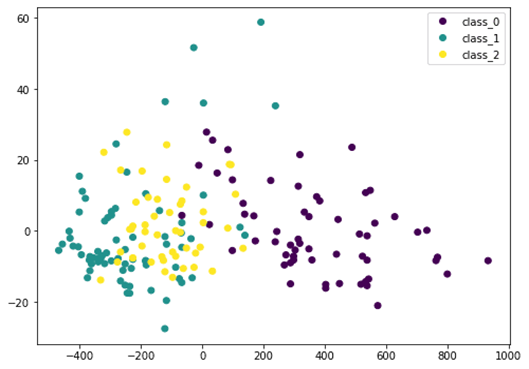
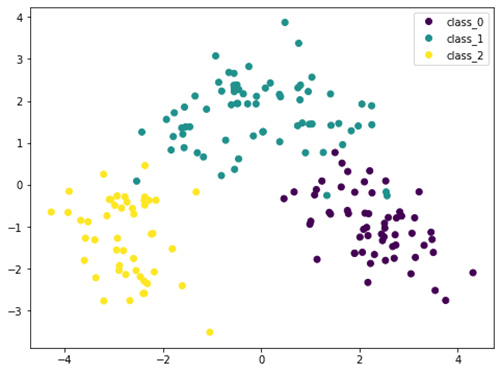
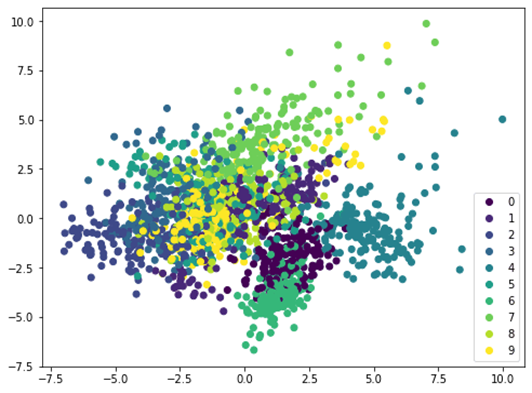
در اینجا داده های ورودی X را توسط PCA به Xt تبدیل می کنیم. ما فقط دو ستون اول را که حاوی بیشترین اطلاعات هستند در نظر می گیریم و آن را به صورت دو بعدی ترسیم می کنیم. می بینیم که کلاس بنفش کاملا متمایز است، اما هنوز همپوشانی هایی (تداخل) وجود دارد. اگر داده ها را قبل از PCA مقیاس بندی کنیم، نتیجه متفاوت خواهد بود:
|
1. … |
| 2. from sklearn.preprocessing import StandardScaler |
| 3. from sklearn.pipeline import Pipeline |
| 4. pca = PCA() |
| 5. pipe = Pipeline([(‘scaler’, StandardScaler()), (‘pca’, pca)]) |
| 6. Xt = pipe.fit_transform(X) |
| 7. plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) |
| 8. plt.legend(handles=plot.legend_elements()[0], labels=list(winedata[‘target_names’])) |
| 9. plt.show() |
از آنجایی که PCA به مقیاس حساس است، اگر هر ویژگی را توسط StandardScaler نرمال سازی کنیم، نتیجه بهتری خواهیم دید. در اینجا کلاس های مختلف متمایز تر هستند. با مشاهده این نمودار، ما مطمئن هستیم که یک مدل ساده مانند SVM می تواند این مجموعه داده را با دقت بالا طبقه بندی کند.
با کنار هم قرار دادن این ها، کد زیر کد کاملی برای تولید تصویر ها است:
|
1. from sklearn.datasets import load_wine |
|
| 2. from sklearn.decomposition import PCA | |
| 3. from sklearn.preprocessing import StandardScaler | |
| 4. from sklearn.pipeline import Pipeline | |
| 5. import matplotlib.pyplot as plt | |
| 6. | |
| 7. # Load dataset | |
| 8. winedata = load_wine() | |
| 9. X, y = winedata[‘data’], winedata[‘target’] | |
| 10. print(“X shape:”, X.shape) | |
| 11. print(“y shape:”, y.shape) | |
| 12. | |
| 13. # Show any two features | |
| 14. plt.figure(figsize=(8,6)) | |
| 15. plt.scatter(X[:,1], X[:,2], c=y) | |
| 16. plt.xlabel(winedata[“feature_names”][1]) | |
| 17. plt.ylabel(winedata[“feature_names”][2]) | |
| 18. plt.title(“Two particular features of the wine dataset”) | |
| 19. plt.show() | |
| 20. | |
| 21. # Show any three features | |
| 22. fig = plt.figure(figsize=(10,8)) | |
| 23. ax = fig.add_subplot(projection=’3d’) | |
| 24. ax.scatter(X[:,1], X[:,2], X[:,3], c=y) | |
| 25. ax.set_xlabel(winedata[“feature_names”][1]) | |
| 26. ax.set_ylabel(winedata[“feature_names”][2]) | |
| 27. ax.set_zlabel(winedata[“feature_names”][3]) | |
| 28. ax.set_title(“Three particular features of the wine dataset”) | |
| 29. plt.show() | |
| 30. | |
| 31. # Show first two principal components without scaler | |
| 32. pca = PCA() | |
| 33. plt.figure(figsize=(8,6)) | |
| 34. Xt = pca.fit_transform(X) | |
| 35. plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) | |
| 36. plt.legend(handles=plot.legend_elements()[0],
labels=list(winedata[‘target_names’])) |
|
| 37. plt.xlabel(“PC1”) | |
| 38. plt.ylabel(“PC2”) | |
| 39. plt.title(“First two principal components”) | |
| 40. plt.show() | |
| 41. | |
| 42. # Show first two principal components with scaler | |
| 43. pca = PCA() | |
| 44. pipe = Pipeline([(‘scaler’, StandardScaler()), (‘pca’, pca)]) | |
| 45. plt.figure(figsize=(8,6)) | |
| 46. Xt = pipe.fit_transform(X) | |
| 47. plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) | |
| 48. plt.legend(handles=plot.legend_elements()[0],
labels=list(winedata[‘target_names’])) |
|
| 49. plt.xlabel(“PC1”) | |
| 50. plt.ylabel(“PC2”) | |
| 51. plt.title(“First two principal components after scaling”) | |
| 52. plt.show() |
اگر روش مشابهی را روی یک مجموعه داده متفاوت مانند ارقام دست نویس MINST اعمال کنیم، نمودار پراکندگی مرز مشخصی را نشان نمی دهد و بنابراین به مدل پیچیده تری مانند شبکه عصبی برای طبقه بندی نیاز دارد:
|
1. from sklearn.datasets import load_digits |
| 2. from sklearn.decomposition import PCA |
| 3. from sklearn.preprocessing import StandardScaler |
| 4. from sklearn.pipeline import Pipeline |
| 5. import matplotlib.pyplot as plt |
| 6. |
| 7. digitsdata = load_digits() |
| 8. X, y = digitsdata[‘data’], digitsdata[‘target’] |
| 9. pca = PCA() |
| 10. pipe = Pipeline([(‘scaler’, StandardScaler()), (‘pca’, pca)]) |
| 11. plt.figure(figsize=(8,6)) |
| 12. Xt = pipe.fit_transform(X) |
| 13. plot = plt.scatter(Xt[:,0], Xt[:,1], c=y) |
| 14. plt.legend(handles=plot.legend_elements()[0], labels=list(digitsdata[‘target_names’])) |
| 15. plt.show() |
تصویر سازی واریانس توضیح داده شده
کار PCA در اصل این است که ویژگی ها را با ترکیب خطی آن ها باز آرایی کند. از این رو به آن تکنیک استخراج ویژگی می گویند. یکی از ویژگی های PCA این است که اولین مؤلفه اصلی بیشترین اطلاعات را در مورد مجموعه داده دارد. دومین مؤلفه اصلی دارای اطلاعات بیشتر از سومین مؤلفه است و غیره.
برای نشان دادن این ایده، میتوانیم مؤلفه های اصلی را از مجموعه داده اصلی مرحله به مرحله حذف کنیم و ببینیم که مجموعه داده چگونه به نظر میرسد. بیایید یک مجموعه داده با ویژگی های کمتر را در نظر بگیریم و دو ویژگی را در یک نمودار نشان دهیم:
|
1. from sklearn.datasets import load_iris |
| 2. irisdata = load_iris() |
| 3. X, y = irisdata[‘data’], irisdata[‘target’] |
| 4. plt.figure(figsize=(8,6)) |
| 5. plt.scatter(X[:,0], X[:,1], c=y) |
| 6. plt.show() |
این مجموعه داده iris است که فقط چهار ویژگی دارد. ویژگی ها در مقیاس های قابل مقایسه هستند و از این رو می توانیم از مقیاس بندی صرف نظر کنیم. با داده های 4 ویژگی، PCA می تواند حداکثر 4 مؤلفه اصلی تولید کند:
|
1. … |
| 2. pca = PCA().fit(X) |
| 3. print(pca.components_) |
| 1. [[ 0.36138659 -0.08452251 0.85667061 0.3582892 ] |
| 2. [ 0.65658877 0.73016143 -0.17337266 -0.07548102] |
| 3. [-0.58202985 0.59791083 0.07623608 0.54583143] |
| 4. [-0.31548719 0.3197231 0.47983899 -0.75365743]] |
به عنوان مثال، ردیف اول اولین محور اصلی است که اولین مؤلفه اصلی بر روی آن ایجاد می شود. برای هر نقطه (پوینت) داده ای “p” با ویژگی p=(a,b,c,d) ، از آن جایی که محور اصلی با بردار (Vector) v=(0.36,-0.08,0.86,0.36) مشخص می شود، اولین مؤلفه اصلی این نقطه داده دارای مقدار
0.36 \times a – 0.08 \times b + 0.86 \times c + 0.36\times d روی محور اصلی است. با استفاده از نتیجه به دست آمده (حاصل ضرب) از نقطه برداری (v)، این مقدار را می توان با
p . v
نشان داد.
بنابراین، با مجموعه داده X به عنوان یک ماتریس 150 × 4 (150 نقطه داده که هر کدام دارای چهار ویژگی است)، میتوانیم هر نقطه داده را به مقدار این محور اصلی با ضرب ماتریس-بردار (matrix-vector) نگاشت کنیم:
X . v
و نتیجه یک بردار به طول 150 است. حال اگر از هر نقطه داده مقدار مربوطه را در امتداد بردار محور اصلی حذف کنیم، این مقدار خواهد بود:
X – (X . v) . vT
که در آن بردار انتقال یافته vT یک ردیف و X یک ستون است. حاصل ضرب
(X . v) . vT ماتریس-ماتریس (matrix-matrix) را دنبال می کند و نتیجه یک ماتریس 150 × 4 است، در همان بٌعد X .
اگر دو ویژگی اول (X . v) . vT را ترسیم کنیم، این گونه به نظر می رسد:
|
1. … |
| 2. # Remove PC1 |
| 3. Xmean = X – X.mean(axis=0) |
| 4. value = Xmean @ pca.components_[0] |
| 5. pc1 = value.reshape(-1,1) @ pca.components_[0].reshape(1,-1) |
| 6. Xremove = X – pc1 |
| 7. plt.scatter(Xremove[:,0], Xremove[:,1], c=y) |
| 8. plt.show() |
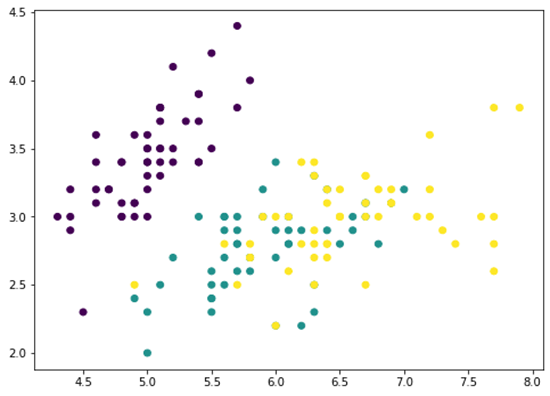
آرایهnumpy Xmean برای تغییر ویژگی های X به مرکز صفر است. این آرایه برای PCA مورد نیاز است. سپس آرایه value با ضرب ماتریس-بردار محاسبه می شود. آرایه value ، مقدار بزرگی هر نقطه داده ای است که روی محور اصلی نگاشته شده است. بنابراین اگر این مقدار را در بردار محور اصلی ضرب کنیم، یک آرایه pc1 برمیگردانیم. با حذف این از مجموعه داده اصلی X ، یک آرایه جدید Xremove دریافت می کنیم. در نمودار مشاهده کردیم که نقاط روی نمودار پراکندگی با هم متلاشی شدند و خوشه هر کلاس کمتر از قبل متمایز است. این بدان معناست که با حذف اولین مؤلفه اصلی، اطلاعات زیادی را حذف کردیم. اگر دوباره همین روند را تکرار کنیم، نقاط بیشتری خرد می شوند:
|
1. … |
| 2. # Remove PC2 |
| 3. value = Xmean @ pca.components_[1] |
| 4. pc2 = value.reshape(-1,1) @ pca.components_[1].reshape(1,-1) |
| 5. Xremove = Xremove – pc2 |
| 6. plt.scatter(Xremove[:,0], Xremove[:,1], c=y) |
| 7. plt.show() |
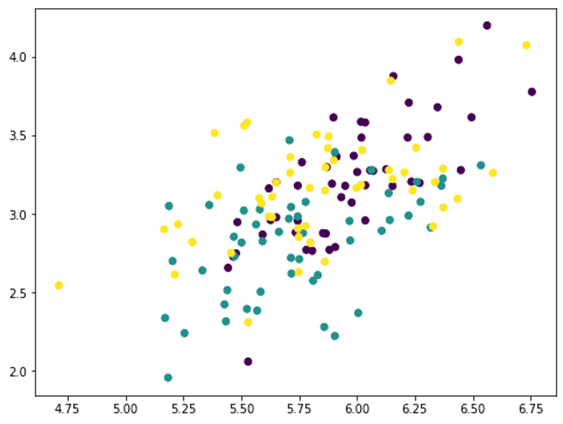
این یک خط صاف به نظر می رسد اما در واقع نیست. اگر یک بار دیگر تکرار کنیم، همه نقاط در یک خط صاف جمع می شوند:
|
1. … |
| 2. # Remove PC3 |
| 3. value = Xmean @ pca.components_[2] |
| 4. pc3 = value.reshape(-1,1) @ pca.components_[2].reshape(1,-1) |
| 5. Xremove = Xremove – pc3 |
| 6. plt.scatter(Xremove[:,0], Xremove[:,1], c=y) |
| 7. plt.show() |
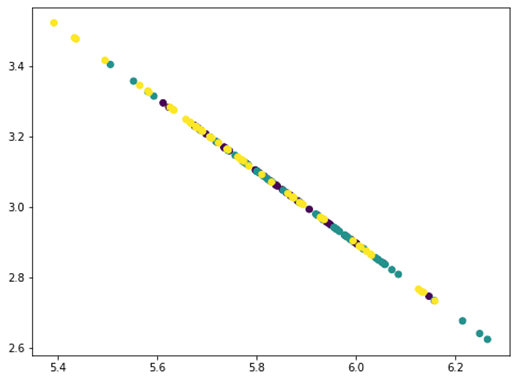
همه نقاط روی یک خط مستقیم قرار میگیرند، زیرا ما سه مؤلفه اصلی را از داده هایی که تنها چهار ویژگی دارند حذف کردیم. از این رو ماتریس داده های ما به rank 1 یا رتبه 1 تبدیل می شود. می توانید یک بار دیگر این فرآیند را تکرار کنید و نتیجه این خواهد بود که همه نقاط در یک نقطه جمع می شوند. مقدار اطلاعات حذف شده در هر مرحله با حذف مؤلفه های اصلی را می توان با نسبت واریانس توضیح داده شده مربوطه از PCA پیدا کرد:
|
1. … |
| 2. print(pca.explained_variance_ratio_) |
| 1. [0.92461872 0.05306648 0.01710261 0.00521218] |
در اینجا می بینیم که مؤلفه اول 92.5 درصد و مؤلفه دوم 5.3 درصد واریانس را توضیح می دهد. اگر دو مؤلفه اصلی اول را حذف کنیم، واریانس باقیمانده تنها 2.2 درصد است، بنابراین از نظر بصری نمودار پس از حذف دو مؤلفه مانند یک خط مستقیم به نظر می رسد. در واقع، وقتی با نمودار های بالا بررسی می کنیم، می بینیم که نه تنها نقاط خرد شده اند، بلکه محدوده محور های x و y نیز با حذف مؤلفه ها کوچکتر می شوند.
از نظر یادگیری ماشینی، میتوانیم تنها از یک ویژگی واحد برای طبقه بندی در این مجموعه داده استفاده کنیم، یعنی اولین مؤلفه اصلی. ما باید انتظار داشته باشیم که با استفاده از مجموعه کامل ویژگی ها، به حداقل 90 درصد از دقت اصلی دست بیابیم:
|
1. … |
| 2. from sklearn.model_selection import train_test_split |
| 3. from sklearn.metrics import f1_score |
| 4. from collections import Counter |
| 5. from sklearn.svm import SVC |
| 6. |
| 7. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33) |
| 8. clf = SVC(kernel=”linear”, gamma=’auto’).fit(X_train, y_train) |
| 9. print(“Using all features, accuracy: “, clf.score(X_test, y_test)) |
| 10. print(“Using all features, F1: “, f1_score(y_test, clf.predict(X_test), average=”macro”)) |
| 11. |
| 12. mean = X_train.mean(axis=0) |
| 13. X_train2 = X_train – mean |
| 14. X_train2 = (X_train2 @ pca.components_[0]).reshape(-1,1) |
| 15. clf = SVC(kernel=”linear”, gamma=’auto’).fit(X_train2, y_train) |
| 16. X_test2 = X_test – mean |
| 17. X_test2 = (X_test2 @ pca.components_[0]).reshape(-1,1) |
| 18. print(“Using PC1, accuracy: “, clf.score(X_test2, y_test)) |
| 19. print(“Using PC1, F1: “, f1_score(y_test, clf.predict(X_test2), average=”macro”)) |
| 1. Using all features, accuracy: 1.0 |
| 2. Using all features, F1: 1.0 |
| 3. Using PC1, accuracy: 0.96 |
| 4. Using PC1, F1: 0.9645191409897292 |
استفاده دیگر از واریانس توضیح داده شده در فشرده سازی است. با توجه به اینکه واریانس توضیح داده شده مؤلفه اول اصلی، بزرگ است، اگر نیاز به ذخیره مجموعه داده داشته باشیم، می توانیم فقط مقادیر تصویر سازی شده در اولین محور اصلی (X . v) و همچنین در بردار v محور اصلی ذخیره کنیم. سپس میتوانیم تقریبا مجموعه داده اصلی را با ضرب آن ها دوباره ایجاد کنیم:
X » (X . v) . vT
به این ترتیب، به جای چهار مقدار برای چهار ویژگی، به ذخیره سازی فقط یک مقدار در هر نقطه داده نیاز داریم. اگر مقادیر تصویر سازی شده را روی محور اصلی چند برابر (multiple) ذخیره کنیم و مؤلفه اصلی را چند برابر کنیم، تقریب دقیق تر است.
با کنار هم قرار دادن این ها، کد زیر برای تولید تصویر سازی ها است:
|
1. from sklearn.datasets import load_iris |
| 2. from sklearn.model_selection import train_test_split |
| 3. from sklearn.decomposition import PCA |
| 4. from sklearn.metrics import f1_score |
| 5. from sklearn.svm import SVC |
| 6. import matplotlib.pyplot as plt |
| 7. |
| 8. # Load iris dataset |
| 9. irisdata = load_iris() |
| 10. X, y = irisdata[‘data’], irisdata[‘target’] |
| 11. plt.figure(figsize=(8,6)) |
| 12. plt.scatter(X[:,0], X[:,1], c=y) |
| 13. plt.xlabel(irisdata[“feature_names”][0]) |
| 14. plt.ylabel(irisdata[“feature_names”][1]) |
| 15. plt.title(“Two features from the iris dataset”) |
| 16. plt.show() |
| 17. |
| 18. # Show the principal components |
| 19. pca = PCA().fit(X) |
| 20. print(“Principal components:”) |
| 21. print(pca.components_) |
| 22. |
| 23. # Remove PC1 |
| 24. Xmean = X – X.mean(axis=0) |
| 25. value = Xmean @ pca.components_[0] |
| 26. pc1 = value.reshape(-1,1) @ pca.components_[0].reshape(1,-1) |
| 27. Xremove = X – pc1 |
| 28. plt.figure(figsize=(8,6)) |
| 29. plt.scatter(Xremove[:,0], Xremove[:,1], c=y) |
| 30. plt.xlabel(irisdata[“feature_names”][0]) |
| 31. plt.ylabel(irisdata[“feature_names”][1]) |
| 32. plt.title(“Two features from the iris dataset after removing PC1”) |
| 33. plt.show() |
| 34. |
| 35. # Remove PC2 |
| 36. Xmean = X – X.mean(axis=0) |
| 37. value = Xmean @ pca.components_[1] |
| 38. pc2 = value.reshape(-1,1) @ pca.components_[1].reshape(1,-1) |
| 39. Xremove = Xremove – pc2 |
| 40. plt.figure(figsize=(8,6)) |
| 41. plt.scatter(Xremove[:,0], Xremove[:,1], c=y) |
| 42. plt.xlabel(irisdata[“feature_names”][0]) |
| 43. plt.ylabel(irisdata[“feature_names”][1]) |
| 44. plt.title(“Two features from the iris dataset after removing PC1 and PC2”) |
| 45. plt.show() |
| 46. |
| 47. # Remove PC3 |
| 48. Xmean = X – X.mean(axis=0) |
| 49. value = Xmean @ pca.components_[2] |
| 50. pc3 = value.reshape(-1,1) @ pca.components_[2].reshape(1,-1) |
| 51. Xremove = Xremove – pc3 |
| 52. plt.figure(figsize=(8,6)) |
| 53. plt.scatter(Xremove[:,0], Xremove[:,1], c=y) |
| 54. plt.xlabel(irisdata[“feature_names”][0]) |
| 55. plt.ylabel(irisdata[“feature_names”][1]) |
| 56. plt.title(“Two features from the iris dataset after removing PC1 to PC3”) |
| 57. plt.show() |
| 58. |
| 59. # Print the explained variance ratio |
| 60. # Print the explained variance ratio |
| 61. print(pca.explained_variance_ratio_) |
| 62. |
| 63. # Split data |
| 64. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33) |
| 65. |
| 66. # Run classifer on all features |
| 67. clf = SVC(kernel=”linear”, gamma=’auto’).fit(X_train, y_train) |
| 68. print(“Using all features, accuracy: “, clf.score(X_test, y_test)) |
| 69. print(“Using all features, F1: “, f1_score(y_test, clf.predict(X_test), average=”macro”)) |
| 70. |
| 71. # Run classifier on PC1 |
| 72. mean = X_train.mean(axis=0) |
| 73. X_train2 = X_train – mean |
| 74. X_train2 = (X_train2 @ pca.components_[0]).reshape(-1,1) |
| 75. clf = SVC(kernel=”linear”, gamma=’auto’).fit(X_train2, y_train) |
| 76. X_test2 = X_test – mean |
| 77. X_test2 = (X_test2 @ pca.components_[0]).reshape(-1,1) |
| 78. print(“Using PC1, accuracy: “, clf.score(X_test2, y_test)) |
| 79. print(“Using PC1, F1: “, f1_score(y_test, clf.predict(X_test2), average=”macro”)) |
خلاصه
در این آموزش، نحوه تصویر سازی داده ها با استفاده از تجزیه و تحلیل مؤلفه های اصلی را یاد گرفتید. به ویژه، یاد گرفتید:
- یک مجموعه داده با ابعاد بالا را به صورت دو بعدی با استفاده از PCA تصویر سازی کنید
- نحوه استفاده از ترسیم (plot) در ابعاد PCA برای کمک به انتخاب یک مدل یادگیری ماشینی مناسب
- نحوه مشاهده نسبت واریانس توضیح داده شده در PCA
- نسبت واریانس توضیح داده شده برای یادگیری ماشینی به چه معناست./

دیدگاهتان را بنویسید